
Next: Choosing a Basis Set
Up: Model
Previous: Basis Functions
Here we are going to describe how we constrain the basis function
linear combinations. To do this we need to reparameterise the
regression parameters,
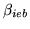 , into parameters which
describe the shape of the HRF, and parameters which scale these
HRF shape parameters, to give the actual fit in the GLM.
Firstly, we specify
, into parameters which
describe the shape of the HRF, and parameters which scale these
HRF shape parameters, to give the actual fit in the GLM.
Firstly, we specify
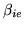 as the
as the
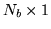 vector of
the regression parameters for the
vector of
the regression parameters for the 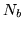 basis functions for the
basis functions for the
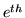 underlying condition at voxel
underlying condition at voxel 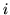 . Then, we
reparameterise
. Then, we
reparameterise
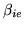 as being:
as being:
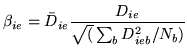 |
|
|
(11) |
where 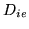 is an
is an
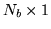 vector of parameters describing
the HRF for underlying condition
vector of parameters describing
the HRF for underlying condition 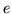 , and
, and
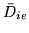 is the
scalar value representing the scaling of that HRF. We want the
scalar
is the
scalar value representing the scaling of that HRF. We want the
scalar
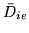 to contain all of our size
information. However, left unchecked there is an arbitrary scale
factor on vector
to contain all of our size
information. However, left unchecked there is an arbitrary scale
factor on vector 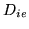 . We have removed this arbitrary scale
factor by normalising the vector using its root mean square.
Hence, we now have a normalised vector,
. We have removed this arbitrary scale
factor by normalising the vector using its root mean square.
Hence, we now have a normalised vector,
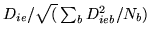 , representing the shape of the HRF, and a scalar,
, representing the shape of the HRF, and a scalar,
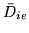 , representing the size of the HRF.
For the scaling parameters we assume a noninformative prior:
, representing the size of the HRF.
For the scaling parameters we assume a noninformative prior:
where the precision,
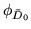 , is fixed to be very small
(1e-6) for all voxels. It is via the prior on
, is fixed to be very small
(1e-6) for all voxels. It is via the prior on 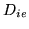 that we can
constrain the possible linear combinations of basis functions to
represent the HRF for an underlying condition. We specify the
prior on
that we can
constrain the possible linear combinations of basis functions to
represent the HRF for an underlying condition. We specify the
prior on 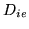 as:
as:
where 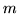 and
and 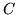 will contain the information constraining the
possible linear combinations of the basis functions (see
section 2.6 for how we set
will contain the information constraining the
possible linear combinations of the basis functions (see
section 2.6 for how we set 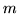 and
and 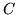 ).
).


Next: Choosing a Basis Set
Up: Model
Previous: Basis Functions