

Next: Results
Up: Validation Tests
Previous: Experimental Tests
Performance was assessed by comparing the correct translation value,
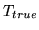 , used to generate the measured image, to the recovered
translation parameter estimate
, used to generate the measured image, to the recovered
translation parameter estimate 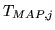 in the
in the 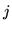 th trial.
th trial.
A measure of the robustness of the estimated translation is:
where 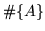 represents the number of elements in set
represents the number of elements in set 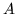 , and
, and
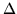 is a moderate tolerance, taken to be 2mm in this case. This
measure represents the fraction of solutions which were not
considered ``close'', where
is a moderate tolerance, taken to be 2mm in this case. This
measure represents the fraction of solutions which were not
considered ``close'', where 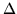 sets the threshold by which
something is considered ``close''.
sets the threshold by which
something is considered ``close''.
A measure of the accuracy of the estimated translation is:
This measure is a modified RMS error measurement, where any errors greater
than 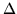 are replaced by
are replaced by 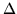 . In this way it downweights the
contribution for very large errors which a non-robust technique can produce
and gives a normalised measure between 0 and 1.
. In this way it downweights the
contribution for very large errors which a non-robust technique can produce
and gives a normalised measure between 0 and 1.
For an ideal method, both measures, 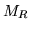 and
and 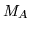 , would be zero.
, would be zero.
![]() , used to generate the measured image, to the recovered
translation parameter estimate
, used to generate the measured image, to the recovered
translation parameter estimate ![]() in the
in the ![]() th trial.
th trial.

![]() and
and ![]() , would be zero.
, would be zero.