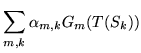

Next: Example
Up: Problem Formulation
Previous: Anatomical Information, Intensities and
Image Generators
The definitions of the image generators are:
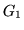 gives an image with an intensity 1.0 for all
voxels totally within the shape, 0.0 for those outside and the partial volume
overlap fraction otherwise;
gives an image with an intensity 1.0 for all
voxels totally within the shape, 0.0 for those outside and the partial volume
overlap fraction otherwise;
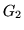 gives an image with an intensity gradient along the
gives an image with an intensity gradient along the
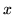 -axis within the shape, with zero values outside. The image is
also demeaned and has partial volume modelled multiplicatively
(i.e.
-axis within the shape, with zero values outside. The image is
also demeaned and has partial volume modelled multiplicatively
(i.e.
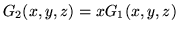 , which is then demeaned);
, which is then demeaned);
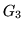 and
and 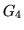 give images with intensity gradients along the
give images with intensity gradients along the
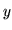 - and
- and 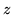 -axes respectively;
-axes respectively;
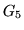 and above can represent other expected image signals
(e.g. quadratic trends, common artifacts, etc.) but will not be used
in this report
and above can represent other expected image signals
(e.g. quadratic trends, common artifacts, etc.) but will not be used
in this report
Note that 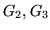 and
and 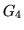 represent the terms that model the
combined effects of bias field and spatially varying tissue
parameters. These are effectively the first terms in the Taylor
series expansion of the general case for bias field and spatially
varying parameters. For shapes with large spatial extent this
approximation may not be sufficiently accurate, in which case it is
possible to include higher-order Taylor series terms (quadratic,
cubic, etc.) via extra
represent the terms that model the
combined effects of bias field and spatially varying tissue
parameters. These are effectively the first terms in the Taylor
series expansion of the general case for bias field and spatially
varying parameters. For shapes with large spatial extent this
approximation may not be sufficiently accurate, in which case it is
possible to include higher-order Taylor series terms (quadratic,
cubic, etc.) via extra 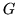 terms (
terms (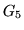 and up).
and up).
These generators are functions, which when applied to a transformed
shape, 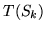 , produce an image containing
, produce an image containing 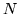 values. The images
are then reshaped into vectors of length
values. The images
are then reshaped into vectors of length 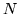 , and assembled into a
single
, and assembled into a
single 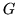 matrix for use in later sections.
matrix for use in later sections.
The image generator can also be written in matrix form:
where 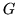 represents an
represents an 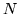 by
by 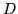 matrix and
matrix and 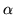 is a column
vector of length
is a column
vector of length 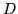 (typically
(typically 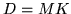 , but will be changed - see
later). Note that in this form
, but will be changed - see
later). Note that in this form 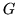 implicitly encodes information
about the transformation
implicitly encodes information
about the transformation 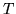 and the underlying shapes,
and the underlying shapes,
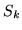 . However, as neither of these will be marginalised, this
dependency is not important for any of the following derivations and
will therefore be left implicit.
. However, as neither of these will be marginalised, this
dependency is not important for any of the following derivations and
will therefore be left implicit.
Subsections


Next: Example
Up: Problem Formulation
Previous: Anatomical Information, Intensities and
![]() and
and ![]() represent the terms that model the
combined effects of bias field and spatially varying tissue
parameters. These are effectively the first terms in the Taylor
series expansion of the general case for bias field and spatially
varying parameters. For shapes with large spatial extent this
approximation may not be sufficiently accurate, in which case it is
possible to include higher-order Taylor series terms (quadratic,
cubic, etc.) via extra
represent the terms that model the
combined effects of bias field and spatially varying tissue
parameters. These are effectively the first terms in the Taylor
series expansion of the general case for bias field and spatially
varying parameters. For shapes with large spatial extent this
approximation may not be sufficiently accurate, in which case it is
possible to include higher-order Taylor series terms (quadratic,
cubic, etc.) via extra ![]() terms (
terms (![]() and up).
and up).
![]() , produce an image containing
, produce an image containing ![]() values. The images
are then reshaped into vectors of length
values. The images
are then reshaped into vectors of length ![]() , and assembled into a
single
, and assembled into a
single ![]() matrix for use in later sections.
matrix for use in later sections.