Consider an image, ![]() , generated by some image generation process,
, generated by some image generation process,
![]() , from a known (ground truth) object,
, from a known (ground truth) object, ![]() , where
, where ![]() is not
spatially aligned with
is not
spatially aligned with ![]() , but related spatially by a transformation,
, but related spatially by a transformation,
![]() . The objective of the segmentation/registration problem is to
recover the spatial transformation,
. The objective of the segmentation/registration problem is to
recover the spatial transformation, ![]() , which relates
, which relates ![]() to
to ![]() .
That is, find
.
That is, find ![]() such that
such that ![]() and
and ![]() are `most
similar'.
are `most
similar'.
A Bayesian formulation of this problem is as follows:
Note that generally ![]() is parameterised by its own set of parameters,
and that
is parameterised by its own set of parameters,
and that ![]() is giving the posterior probability for these
transformation parameters.
is giving the posterior probability for these
transformation parameters.
The probabilities are related by:
| (1) | |||
| (2) | |||
| (3) |
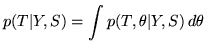 |
(4) |
Note that marginalising over ![]() is the difficult step in
calculating
is the difficult step in
calculating ![]() .
.
The problem of finding the `best' single segmentation/registration1 is then equivalent to finding the maximum a-posterior probability: the MAP estimate.
That is:
Therefore ![]() , or
, or
![]() , play an equivalent role to
the similarity function in common registration techniques.
, play an equivalent role to
the similarity function in common registration techniques.