Consider two transformations, ![]() and
and ![]() , each mapping volume A
to volume B (the reference volume). Now a point in volume A,
, each mapping volume A
to volume B (the reference volume). Now a point in volume A, ![]() (a
three vector), is mapped to some point in volume B by each
transformation. If the transformations are identical then the points
in volume B will be the same. However, in general the transformations
differ and so map
(a
three vector), is mapped to some point in volume B by each
transformation. If the transformations are identical then the points
in volume B will be the same. However, in general the transformations
differ and so map ![]() to two different points:
to two different points: ![]() and
and
![]() . The vector difference between these points,
. The vector difference between these points,
![]() , represents the error in the transformation. It is the
average magnitude of this error that is of interest.
, represents the error in the transformation. It is the
average magnitude of this error that is of interest.
As world coordinates are being used, the magnitude of the error vector,
![]() is the magnitude of the deviation expressed in millimetres.
Therefore some average of this quantity will express the desired average
error. Here the root mean square measure is chosen as the desired average
since it is easier to deal with analytically.
is the magnitude of the deviation expressed in millimetres.
Therefore some average of this quantity will express the desired average
error. Here the root mean square measure is chosen as the desired average
since it is easier to deal with analytically.
In addition, the volume of interest for the average must be defined. For measuring the average error over the brain volume a spherical volume is the simplest approximation. A cubic volume is obviously a worse approximation and will tend to be dominated by the error near the corners, which for a rotational error increases with the distance from the centre of the cube.
Using homogeneous coordinates1 the error vector can be written in matrix form
as:
In general, the general form
![]() can be used to give the
squared error:
can be used to give the
squared error:
The normalised RMS error is then given by:
| (8) |
Expanding equation 7 for spherical coordinates, ![]() where
where
![]() , gives:
, gives:
| (9) |
| (10) |
Now integrating over the desired spherical volume
![]() gives:
gives:
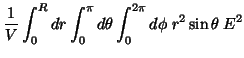 |
(11) | ||
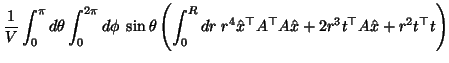 |
(12) | ||
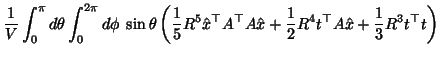 |
(13) |
Denoting
![]() and
and
| (14) |
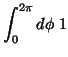 |
(15) | ||
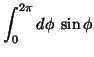 |
(16) | ||
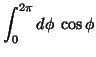 |
(17) | ||
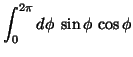 |
(18) | ||
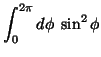 |
(19) | ||
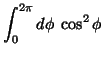 |
(20) | ||
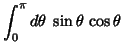 |
(21) | ||
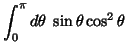 |
(22) | ||
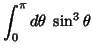 |
(23) |
| (24) | |||
| (25) | |||
| (26) |
Furthermore, by expanding the matrix product,
| (27) |
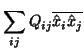 |
(28) | ||
| (29) | |||
| (30) |
Therefore, by substituting the above results, the RMS error is given by:
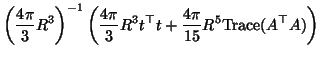 |
(31) | ||
| (32) |