


Next: Hypothesis testing and Estimability
Up: General Linear Model
Previous: General Linear Model
Let 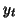 , be the time series observed from
, be the time series observed from 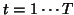 , at a given voxel, this is represented
as a vector on
, at a given voxel, this is represented
as a vector on 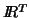 ;
; 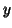 is a
is a 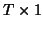 vector. The relationship between the observed time
series and the paradigm of the experiment ( with any other covariates) is expressed as:
vector. The relationship between the observed time
series and the paradigm of the experiment ( with any other covariates) is expressed as:
where 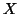 is a
is a 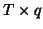 matrix representing the design and the
covariates,
matrix representing the design and the
covariates, 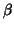 is a
is a 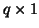 vector of parameters (expressing the linear
relationship)9 and
vector of parameters (expressing the linear
relationship)9 and 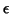 is a
is a
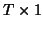 vector of random errors (departure from the model or residuals) assumed identically
distributed (independent or not independent) with mean 0 and common variance
vector of random errors (departure from the model or residuals) assumed identically
distributed (independent or not independent) with mean 0 and common variance 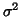 . That will
make the distribution of the vector
. That will
make the distribution of the vector 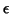 with mean 0 and variance covariance matrix
with mean 0 and variance covariance matrix
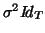 if independent10 or
if independent10 or 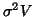 , V being then the autocorrelation matrix
(supposed to be known in this section).
One usual way to estimate
, V being then the autocorrelation matrix
(supposed to be known in this section).
One usual way to estimate 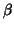 is by Least Squares of the
``residuals''11:
is by Least Squares of the
``residuals''11:
![\begin{displaymath}\widehat{\beta}=arg\min_\beta [^t(y-X\beta)(y-X\beta)]\end{displaymath}](img131.gif) |
(14) |
This problem can be solved by taking partial derivatives; this leads to
the so called normal equation
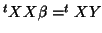 and to a solution using
the inverse or g-inverse12 of
and to a solution using
the inverse or g-inverse12 of 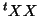 :
:
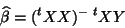 |
(15) |
This is called the ordinary least squares (OLS) estimate, and if the errors are independent
(
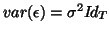 ) according to Gauss-Markov theorem13
[11][3] it is the best linear unbiased estimate (BLUE) of
) according to Gauss-Markov theorem13
[11][3] it is the best linear unbiased estimate (BLUE) of 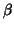 which means that its mean (expectation) is
which means that its mean (expectation) is 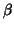 and the estimate is of minimum variance (among
the linear unbiased estimates14):
and the estimate is of minimum variance (among
the linear unbiased estimates14):
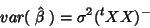 |
(16) |
If
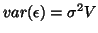 ,
, 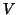 can be replaced with
can be replaced with 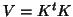 (if
(if 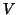 is positive definite
is positive definite 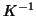 exists15),
applying
exists15),
applying 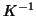 to the GLM gives the model:
to the GLM gives the model:
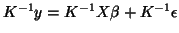 meeting the Gauss-Markov
properties. The OLS estimate of
meeting the Gauss-Markov
properties. The OLS estimate of 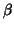 is then written:
is then written:
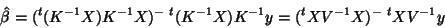 |
(17) |
and rewriting the optimisation problem shows that this is the solution of
![$\min_\beta
[^t(y-X\beta)V^{-1}(y-X\beta)]$](img144.gif) called the Generalised Least Squares (GLS)16. One has also
called the Generalised Least Squares (GLS)16. One has also
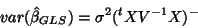 |
(18) |
Remark:
When
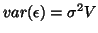 ,
,
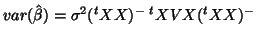 , then the
OLS is BLUE if and only if
, then the
OLS is BLUE if and only if
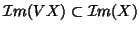 (the space generated by VX is
included in the one generated from X); so in that case OLS
(the space generated by VX is
included in the one generated from X); so in that case OLS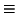 GLS [12].
GLS [12].



Next: Hypothesis testing and Estimability
Up: General Linear Model
Previous: General Linear Model
Didier Leibovici
2001-03-01