- ...
maxima)1
- The point distribution is the distribution at a given voxel, i.e. one
random variable, and the field distribution is the continuous version of multivariate distribution
i.e. a distribution of a vector of random variables.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... voxel2
- The only
spatial consideration comes when thresholding the statistic map.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... autocorrelation3
- Looking for robust estimates of the
autocorrelation can be achieved by using a robust estimate for each time series, and by smoothing
spatially the autocorrelation obtained.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (i.i.d.)4
- Note
that independence for a time series is not realistic and autocorrelation has to be taken into
account, see further.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... activation)5
- As already indicated in the introduction, this level of decision is said
to be uncorrected as based on the point distribution and not using the field distribution
(multiple comparison problem).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... assumption:6
- It is valid
as a conditional distribution (conditionally to the given subject). A fixed factor (ANOVA
language) means that all levels of the factor (here the different subjects) encompass the possible
levels one can encounter in the population studied; e.g. gender is a fixed factor with two
levels.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
statistics:7
- If one supposes equality of ``estimated
variances''
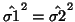 and
and 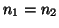 , like
a ``Group Z'', one obtains
, like
a ``Group Z'', one obtains
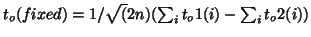 or
or
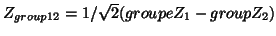 or
or
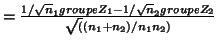 if
if
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
comparisons8
- Although Hotelling's
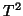 might be used at
this stage
might be used at
this stage
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
relationship)9
- As a trivial illustration of the link with the first section, let
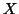 have
two columns; one column containing 1 when the condition is A and 0 otherwise (this column
identifies condition A), and one column identifying B, then
have
two columns; one column containing 1 when the condition is A and 0 otherwise (this column
identifies condition A), and one column identifying B, then
 is going to be
the activation looked for, as an estimate of the difference of the means.
is going to be
the activation looked for, as an estimate of the difference of the means.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... independent10
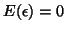 and
and
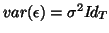 are
called the Gauss-Markov conditions.
are
called the Gauss-Markov conditions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
``residuals''11
- To obtain the best estimate one wants to
minimise the variation between what is observed (
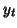 ) and what
is modelled (
) and what
is modelled (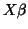 )
)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... g-inverse12
- Generalised inverse
[12] is used when
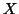 is not of full rank giving a non-invertible
is not of full rank giving a non-invertible 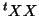 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... theorem13
- The Gauss-Markov
theorem is in fact established for any estimable function (see further) of
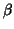 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... estimates14
- It can be shown that for independent Normally distributed
errors, the OLS is also the maximum likelihood BUE
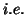 among all estimates.
among all estimates.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... exists15
- If
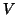 is
only semi-definite positive (and thus singular) everything is done
with g-inverses,
is
only semi-definite positive (and thus singular) everything is done
with g-inverses,
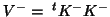 , the BLUE property remains if
and only if
, the BLUE property remains if
and only if  [11][12].
[11][12].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (GLS)16
- When
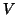 is
known
is
known
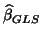 is also BLUE and BUE under Normality.
is also BLUE and BUE under Normality.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... estimate17
- Or more generally with
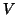 singular[3]
singular[3]
 where
where
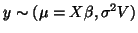 and
and 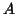 is the resulting from the quadratic form of the residuals,
is the resulting from the quadratic form of the residuals,
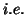
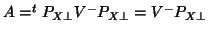 then giving
then giving
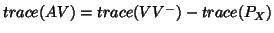 giving
giving 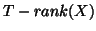 if
if 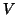 non-singular [12].
non-singular [12].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... statistic18
- The distribution given (exact is
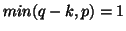 ) is a traditional McKeon(1974)Biometrika,
61:381-383 approximate distribution, where
) is a traditional McKeon(1974)Biometrika,
61:381-383 approximate distribution, where
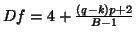 and
and
 ,
and
,
and
![$\nu=((q-k)p)[\frac{Df-2}{Df}][\frac{rank(P_{X\bot})}{(rank(P_{X\bot})-p-1)}]$](img185.gif)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... BLUE)19
- The situation is
less critical in a number of cases where the covariance structure is known and few parameters have
to be estimated.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... estimated-GLS20
- It is nonetheless possible to do
this for fMRI studies with the hypothesis of the same
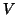 for all of the voxels, so giving a large
sample to estimate
for all of the voxels, so giving a large
sample to estimate 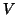 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... anymore:21
- Notice that GLS brings one back to OLS under a
Gauss-Markov model assumption.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... freedom22
- if
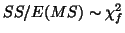 then
then
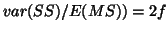 hence
hence

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
approximatively23
- It would be exact if
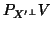 was
idempotent [12] making
was
idempotent [12] making
 as well.
as well.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... assumption24
- Without ``swamping"
the formulae given above for
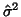 and (26) still hold if
and (26) still hold if 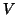 is replaced by
is replaced by
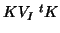 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
errors25
- Note in all the text
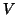 is sometimes expressing
the covariance structure and sometimes only the correlation
structure; no distinction has been made and it should be clear
enough, noting that usually here common variance is assumed and so
the same scalar
is sometimes expressing
the covariance structure and sometimes only the correlation
structure; no distinction has been made and it should be clear
enough, noting that usually here common variance is assumed and so
the same scalar 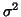 enables one to go from one to
another.
enables one to go from one to
another.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variables)26
- This is if only random intercepts are
considered, one may consider all parameters in
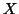 as random, making
as random, making
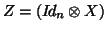
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variation27
- Compound Symmetry is the covariance model used in the
section 3.2,

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... thing)28
- and the projectors are expressed with or without the
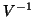 according BLUE or not
BLUE.
according BLUE or not
BLUE.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... parameters29
- Instead of averaging the variances of the
parameters one may median or max depending on how we want to be conservative or not.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... GLS30
- Alternatively
estimating
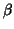 given the whole covariance, and estimating covariances (different levels) given
given the whole covariance, and estimating covariances (different levels) given
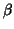 , is known to converge to the maximum likelihood estimates under normality.
, is known to converge to the maximum likelihood estimates under normality.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... projector31
- Really,
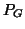 should be denoted
should be denoted ![$P_{[G]}$](img411.gif) , the projector
onto the space generated by the columns of
, the projector
onto the space generated by the columns of 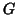 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....32
- Note that
 and if
and if
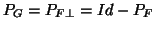 , it is equal to
, it is equal to
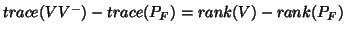
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.