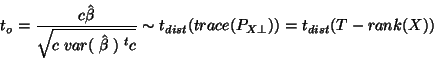Next: Taking into account the
Up: General Linear Model
Previous: The model for single-subject
Now assuming Normal distribution of errors one has a Normal distribution for the parameter vector
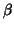 which in this section is supposed to be the BLUE; then to test a hypothesis of the form
which in this section is supposed to be the BLUE; then to test a hypothesis of the form
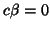 where
where  is a
is a 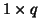 vector, the following statistic is used:
vector, the following statistic is used:
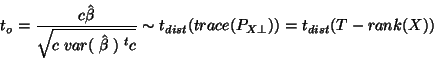 |
(19) |
with the unbiased estimate17
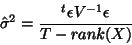 |
(20) |
The reader
can check that taking 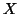 with 2 columns one of 1 everywhere and the other of 1 and -1 whether
under condition B or A;
with 2 columns one of 1 everywhere and the other of 1 and -1 whether
under condition B or A;
 , choosing
, choosing 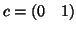 gives the same
gives the same 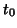 shown in the single-subject analysis section.
Only
shown in the single-subject analysis section.
Only  which are estimable can be used in the testing procedure. A linear function of
the parameter
which are estimable can be used in the testing procedure. A linear function of
the parameter  is said to be estimable if a linear unbiased estimate exists:
is said to be estimable if a linear unbiased estimate exists:
and this is if and only if 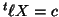 . This makes
. This makes
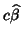 a unique BLUE of
a unique BLUE of  .
Contrasts are particular estimable linear functions with the additional property that
.
Contrasts are particular estimable linear functions with the additional property that 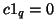 ,
where
,
where
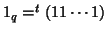 , i.e. the sum of the entries (weights) in the contrast is zero.
This definition holds for more general hypothesis testing when
, i.e. the sum of the entries (weights) in the contrast is zero.
This definition holds for more general hypothesis testing when 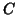 is
a
is
a  matrix of
matrix of 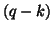 independent linear estimable
functions. The following statistic (with distribution under
independent linear estimable
functions. The following statistic (with distribution under 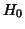 )
called the Lawley-Hotelling trace is used to test the general
hypothesis
)
called the Lawley-Hotelling trace is used to test the general
hypothesis 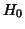 ;
;  :
:
This statistic 18 is in fact for Multivariate GLM, i.e. when 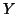 is a matrix
is a matrix
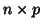 of
of 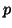 variables
variables
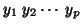 . In our
case
. In our
case 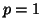 and
and 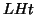 reduces to the traditional
reduces to the traditional 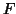 ratio
statistic:
ratio
statistic:
![\begin{displaymath}
F=\frac{(^t(C\hat{\beta})[C(^t(XV^{-1}X)^-{\;}^tC]^-C\hat{\beta}}{(q-k)\hat{\sigma}^2}\sim
F_{(q-k,rank(P_{X\bot}))}\end{displaymath}](img192.gif) |
(22) |
Writing
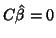 as:
as:

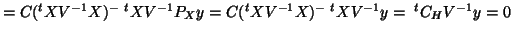 ;
denoting
;
denoting
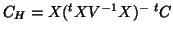 ;
; 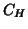 generates what is
called in the appendix the conditioned model, then the
numerator of the F statistic given in the appendix
generates what is
called in the appendix the conditioned model, then the
numerator of the F statistic given in the appendix
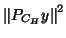 is the numerator given here.
As an example the
is the numerator given here.
As an example the 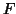 statistic can be used in a single subject
analysis with a paradigm having more than two conditions (ON and
OFF) but different levels for the ON conditions, like different
audio stimuli.
Remarks:
Notice that the statistic (22) can be written:
statistic can be used in a single subject
analysis with a paradigm having more than two conditions (ON and
OFF) but different levels for the ON conditions, like different
audio stimuli.
Remarks:
Notice that the statistic (22) can be written:
called Wald's type statistic.
This form is simple and then advantageous to be used directly in any context. In the
Lawley-Hotelling trace statistic, one must also note that
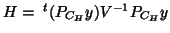 ,
sometimes called the hypothesis statistic (
,
sometimes called the hypothesis statistic ( being the error statistic) and can be derived also
using the form
being the error statistic) and can be derived also
using the form
![$(^t(C\hat{\beta})[var(C\hat{\beta)}]^-C\hat{\beta} \times \sigma^2$](img202.gif) : with OLS
estimate,
: with OLS
estimate,
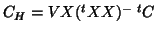 generates the conditioned model. When not considering the BLUE
of
generates the conditioned model. When not considering the BLUE
of 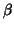 their distributions are then approximated (see next section for estimates of the
degrees of freedom for the denominator).
their distributions are then approximated (see next section for estimates of the
degrees of freedom for the denominator).



Next: Taking into account the
Up: General Linear Model
Previous: The model for single-subject
Didier Leibovici
2001-03-01