


Next: Alternatives to the Random
Up: Multi-subject analysis
Previous: Random Subject Analysis
Notice that
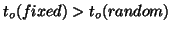 ; the difference may be quite
large, as the between-subject variation is normally much larger
than the within-subject variation (scan-to-scan). Sample size must
be considered here, as to be able to give an accurate decision
about the population (as with the random-effects analysis) one
needs a good estimate of the between-subject variation.
There is also a difference in the degrees of freedom:
; the difference may be quite
large, as the between-subject variation is normally much larger
than the within-subject variation (scan-to-scan). Sample size must
be considered here, as to be able to give an accurate decision
about the population (as with the random-effects analysis) one
needs a good estimate of the between-subject variation.
There is also a difference in the degrees of freedom:
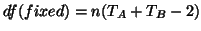 , and
, and
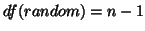 . As a rule, with more general models, the degrees
of freedom for a fixed-effect approach will be the sum of the degrees of freedom from every
single-subject analysis and the degrees of freedom for a random-effect approach will be the
degrees of freedom of the second stage model (explained further in the GLM section). Notice the
very low
. As a rule, with more general models, the degrees
of freedom for a fixed-effect approach will be the sum of the degrees of freedom from every
single-subject analysis and the degrees of freedom for a random-effect approach will be the
degrees of freedom of the second stage model (explained further in the GLM section). Notice the
very low 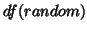 compared with the fixed-effects approach (a typical
compared with the fixed-effects approach (a typical 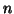 is 10, and
is 10, and 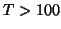 ).
The random-effects approach is the valid one but is difficult to be confident in (power analysis)
as the sample size used in general is very small compared to what is usually needed in estimation
(say at least 30). For fMRI studies it has been suggested that 12 to 15 subjects would suffice.
From a large sample (
).
The random-effects approach is the valid one but is difficult to be confident in (power analysis)
as the sample size used in general is very small compared to what is usually needed in estimation
(say at least 30). For fMRI studies it has been suggested that 12 to 15 subjects would suffice.
From a large sample (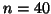 ), Darrell et. al (1998)[4] presented a power analysis
resulting in sufficient power observed for about 20 subjects (depending on the brain area under
consideration). A possible alternative way of obtaining more degrees of freedom (and so a better
estimation) would be to estimate the random variance needed using more data that is on the whole
brain, for example by pooling or smoothing the variances. This is similar to the idea used by
Worsley in the ``variance ratio method'' described in the next section.
), Darrell et. al (1998)[4] presented a power analysis
resulting in sufficient power observed for about 20 subjects (depending on the brain area under
consideration). A possible alternative way of obtaining more degrees of freedom (and so a better
estimation) would be to estimate the random variance needed using more data that is on the whole
brain, for example by pooling or smoothing the variances. This is similar to the idea used by
Worsley in the ``variance ratio method'' described in the next section.



Next: Alternatives to the Random
Up: Multi-subject analysis
Previous: Random Subject Analysis
Didier Leibovici
2001-03-01