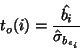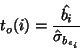Next: Fixed Subject Analysis
Up: tr00dl1
Previous: Single-Subject Analysis
Multi-subject analysis
Because of the separability aspect of the analysis, one easy implementation is to perform a
two-stage procedure. At the first stage the analysis above is performed for each of the 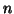 subjects: following the previous section (or, for the more general case, see the GLM section), at
each voxel an estimation of activation parameter can be made:
subjects: following the previous section (or, for the more general case, see the GLM section), at
each voxel an estimation of activation parameter can be made:
 with standard error
with standard error
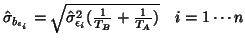 .
.
So for each of the 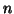 subjects can be built the statistic map
subjects can be built the statistic map
to test 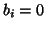 . How do we combine these maps to conclude that
there is activation in the population from which these subjects come? This is the purpose of
multi-subject analysis, i.e. the second stage. From the experiment a different conclusion
is drawn for the population according to the method chosen: fixed subject effect analysis allows a
conclusion limited to the sample studied; a random subject effect allows a population conclusion.
Because the latter can be ``too conservative'' due to large estimated subject-subject variability
(partially due to small sample sizes generally studied ), some alternative approaches have also
been developed: ``conjunction analysis'', and ``variance ratio smoothing''.
. How do we combine these maps to conclude that
there is activation in the population from which these subjects come? This is the purpose of
multi-subject analysis, i.e. the second stage. From the experiment a different conclusion
is drawn for the population according to the method chosen: fixed subject effect analysis allows a
conclusion limited to the sample studied; a random subject effect allows a population conclusion.
Because the latter can be ``too conservative'' due to large estimated subject-subject variability
(partially due to small sample sizes generally studied ), some alternative approaches have also
been developed: ``conjunction analysis'', and ``variance ratio smoothing''.
Subsections



Next: Fixed Subject Analysis
Up: tr00dl1
Previous: Single-Subject Analysis
Didier Leibovici
2001-03-01