


Next: Degrees of freedom and
Up: Multi-subject analysis
Previous: Fixed Subject Analysis
Random Subject Analysis
The inadequacy of the fixed-effects approach is seen in the first assumption:6
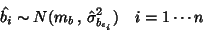 |
(6) |
One must consider the estimated
activation as what it is, an estimation of the activation for the given subject:
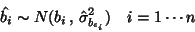 |
(7) |
and now
consider the activation for a given subject as a random
observation of the activation for the population:
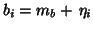 ,
, 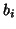 is random
is random
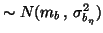 .
.
It is a two levels variation
(within subject and between subjects): before, one had
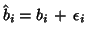 , now:
, now:
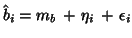 , i.e. two
error terms.
, i.e. two
error terms.
So,
 and testing
and testing 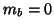 is a one sample
is a one sample 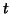 -test:
-test:
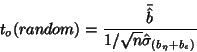 |
(8) |
Note that only the whole variation is needed, as one is not interested in the individual variance
components. The whole variation is calculated directly using the set of estimated single-subject
activation levels (the 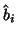 's) as
's) as
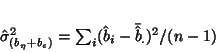 |
(9) |
which usually will reflect mainly the between-subject variation.
Remarks:
Notice here that introducing the random effects for the subject brings a constant autocorrelation
between time measures (Compound Symmetry): let 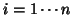 and
and 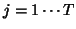 identifying
respectively the subjects and the time of measurements; the model can be written
identifying
respectively the subjects and the time of measurements; the model can be written
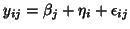 with
with 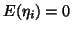 ,
,
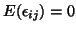 ,
,
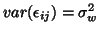 ,
and
,
and
 then
then
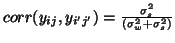 for
for 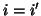 .
.



Next: Degrees of freedom and
Up: Multi-subject analysis
Previous: Fixed Subject Analysis
Didier Leibovici
2001-03-01