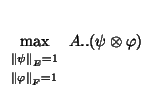

Next: -modes Correspondence Analysis
Up: tr00dl2
Previous: Supplementary points
The general method of SVD-kmodes can be performed with non-identity metrics. This means that
inner products can be considered weighted (diagonal metrics) or cross-weighted (non-diagonal
metrics). The whole algebraic setup used at the beginning of the paper is the same if one
understands the contracted product (operation ..) as containing the metrics. For example,
equations (5) expressing the classic SVD become :
where spaces  and
and  have now respectively the metrics
have now respectively the metrics 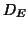 and
and 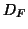 (instead of the
identity metrics). The only change is in the last expression (matrix form) because the metrics are
``included" in the contracted product operation as well as in the norms (as defined from the inner
product) ; equation (6) is as well :
(instead of the
identity metrics). The only change is in the last expression (matrix form) because the metrics are
``included" in the contracted product operation as well as in the norms (as defined from the inner
product) ; equation (6) is as well :
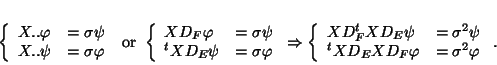 |
(17) |
Consideration of metrics offers flexibility to the analysis. For example with two modes it is
classical to recognise a discriminant analysis as a SVD on the projected data with 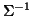 (the inverse of the covariance matrix) as metric on the space defined by the variables or as a SVD
of the original data with
(the inverse of the covariance matrix) as metric on the space defined by the variables or as a SVD
of the original data with 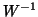 , the inverse of the within covariance matrix. Roughly speaking,
when looking for ``best directions", directions of high within variation have a lower
weight than the other directions (see also [2] when the group structure is not
known). Another good example of non-identity metrics is also in the next section, correspondence
analysis. Nonetheless the method offers the possibility only of decomposed whole space metrics,
i.e. of the form:
, the inverse of the within covariance matrix. Roughly speaking,
when looking for ``best directions", directions of high within variation have a lower
weight than the other directions (see also [2] when the group structure is not
known). Another good example of non-identity metrics is also in the next section, correspondence
analysis. Nonetheless the method offers the possibility only of decomposed whole space metrics,
i.e. of the form:
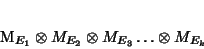 |
(18) |
where every metrics as algebraic object (self-adjoint linear operator) is confounded with its
definite or semi-definite positive matrix representation (like 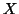 as tensor and array or vector).
The tensor product operation is the one for linear operators (see also [4]). It is
left with the same notation (as for vectors) because it is possible to confound the algebraic
notation and arithmetic, as well . This is because it becomes the Kronecker tensor product
sometimes called the outer product which operates either on vectors or matrices. One must note
that (18) is a linear operator onto the whole space,which operates separately onto every
space defining the tensor space (this is in fact the definition of the tensor product of linear
operators). Arithmetically and computationally this can be written:
as tensor and array or vector).
The tensor product operation is the one for linear operators (see also [4]). It is
left with the same notation (as for vectors) because it is possible to confound the algebraic
notation and arithmetic, as well . This is because it becomes the Kronecker tensor product
sometimes called the outer product which operates either on vectors or matrices. One must note
that (18) is a linear operator onto the whole space,which operates separately onto every
space defining the tensor space (this is in fact the definition of the tensor product of linear
operators). Arithmetically and computationally this can be written:
Without knowing the decomposition of 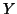 , this last expression cannot be used, nonetheless
isomorphism properties within multilinear maps (tensor) can be used to perform successively the
different operators (e.g.
, this last expression cannot be used, nonetheless
isomorphism properties within multilinear maps (tensor) can be used to perform successively the
different operators (e.g.
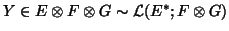 then 19 is equivalent to
then 19 is equivalent to
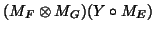 where
where 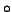 stands for
composition of applications or matrix multiplication). The contraction product includes the
metrics using this property and could also have been understood as a canonical contraction product
(without metrics) of the transformed tensor (the contracting one) by the metric operators,
i.e. the canonical contraction would be using only the dual product instead of the inner product:
stands for
composition of applications or matrix multiplication). The contraction product includes the
metrics using this property and could also have been understood as a canonical contraction product
(without metrics) of the transformed tensor (the contracting one) by the metric operators,
i.e. the canonical contraction would be using only the dual product instead of the inner product:
![\begin{displaymath}
Y..z=Y.._c (M_E z)=[Y \circ M_E ] .._c z
\end{displaymath}](img234.gif) |
(20) |
What is a good choice of metrics for pharmaco-EEG studies ? Generally Choices are geared towards
``elimination" of unwanted variation, such as in discriminant analysis one do not want to relate
the within group variation. For pharmaco-EEG data it would be interesting to eliminate natural
variation of bands and electrodes as well as within dose variation. To achieve estimation of
natural variation, enough placebo observations or better some ``null" data on the subjects
studied are needed. Metric choice and their estimation is a key issue in multidimensional and/or
multiway analysis particularly for this kind of data and deserves more attention (see
[15]).


Next: -modes Correspondence Analysis
Up: tr00dl2
Previous: Supplementary points
Didier Leibovici
2001-09-04