Consider two types of extreme (or asymptotic) registrations:
Both of these cases represent poor registrations and it is therefore important that the cost values associated with them are high. If this is not the case then the global minimum may be associated with these transformations rather than the desired one, violating the first assumption outlined in section 2.5. Furthermore, limiting the domain to exclude these transformations will only eliminate the problem if the cost at the domain boundary is guaranteed to be larger than the global minimum, which is generally difficult or impossible to do as the value at the global minimum is unknown.
In examining the asymptotic behaviour it is important to define what the boundary conditions are. That is, what is done for points in space which do not lie in one or other of the volume domains. One option is to (conceptually) pad the volumes with zeros to give them infinite domain. However, this creates artificial intensity boundaries when the FOV only includes part of the head (for example, when the top few mm of the head/brain are not included the intensity suddenly drops from that of brain matter to zero) -- which is relatively common. These artificial boundaries would then bias the registration, which is undesirable. Therefore, a better alternative is to only calculate the cost function for the region where the volumes overlap. This usually requires some extra calculations in practice, as the normalisation now depends on the overlap volume, which depends on the transformation, but the resulting registration is, in theory, unbiased.
The cost functions that will be compared here are:
the Woods function [Woods et al., 1993], Correlation Ratio [Roche et al., 1998],
Joint Entropy [Studholme et al., 1995,Collignon et al., 1995], Mutual
Information [Viola and Wells, 1997,Maes et al., 1997], and Normalised Mutual
Information [Studholme et al., 1999,Maes, 1998]. Denoting the two images by
X (typically Ir) and Y (typically
![]() ), the respective
cost functions1 are defined as:
), the respective
cost functions1 are defined as:
| CW | = | 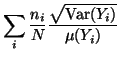 |
(7) |
| CCR | = | (8) | |
| CJE | = | H(X,Y) | (9) |
| CMI | = | H(X,Y) - H(X) - H(Y) | (10) |
| CNMI | = | 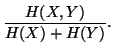 |
(11) |
Here the quantities X and Y represent the images as the set of
intensities evaluated at the discrete, valid grid points. That is,
![]() where G represents the discrete grid and
where G represents the discrete grid and
![]() the continuous,
valid domain (that is, the FOV). Also:
the continuous,
valid domain (that is, the FOV). Also:
These definition require the specification of a partition of the
intensities:
![]() .
This partition is used
to define the various histograms and iso-sets required for the
calculation of the cost functions. In particular, a discrete bin (or
iso-set) number is calculated for each voxel using the intensity at
that voxel. For example, at location q in image X the intensity
is X(q) and the bin number is k if
Ik < X(q) < Ik+1.
Then, given this bin number, iso-sets or the joint histogram are easily
determined.
.
This partition is used
to define the various histograms and iso-sets required for the
calculation of the cost functions. In particular, a discrete bin (or
iso-set) number is calculated for each voxel using the intensity at
that voxel. For example, at location q in image X the intensity
is X(q) and the bin number is k if
Ik < X(q) < Ik+1.
Then, given this bin number, iso-sets or the joint histogram are easily
determined.
That is, the kth iso-set, Yk, is the set of Y intensities where the corresponding voxel in X has a bin number k -- the intensity X(q) is between Ik and Ik+1. The joint histogram is composed of a number of elements, where the element b(i,j)represents the number of voxels where the intensity of X is in the ith bin, (Ii,Ii+1), and the intensity of Y for the same (corresponding) voxel is in the jth bin, (Ij,Ij+1). The probability associated with this element pij is then simply the value of the element divided by the sum of all the elements.
Furthermore, for each of these cost functions the range can easily be
determined, and is:
| (12) | |||
| (13) | |||
| (14) | |||
| (15) | |||
| (16) |