| CW | 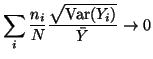 |
(23) | |
| CCR | |||
| (24) | |||
| CJE | = | (25) | |
| CMI | H(X) - H(X) - 0 = 0 | (26) | |
| CNMI | 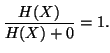 |
(27) |
In this case a small portion of the floating volume is stretched to
cover the reference volume.2 Therefore the
floating volume (Y) is approximately constant over the volume of
overlap. Consequently:
| CW | 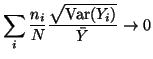 |
(23) | |
| CCR | |||
| (24) | |||
| CJE | = | (25) | |
| CMI | H(X) - H(X) - 0 = 0 | (26) | |
| CNMI | 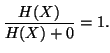 |
(27) |
Once again, the Woods function and Joint Entropy give low cost values indicating a good registration, and so are likely to violate the assumption (stated in section 2.5) that the global minimum is the desired solution. Consequently, these functions should not be used. Note that although the Joint Entropy does not approach zero, the value is H(X) = H(X,X) which is the same as it would be for a perfect registration of the volume with itself.
Overall, only the Correlation Ratio, Mutual Information and Normalised Mutual Information display the correct asymptotic behaviour and therefore these are the only suitable cost functions (from this selection) to use.