To estimate the smoothing variances,
![]() ,
the expectation of the partial derivative is used. That is,
,
the expectation of the partial derivative is used. That is,
This follows easily from equations 28 and 14
by setting
![]() . That is:
. That is:
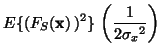 |
(31) | ||
| (32) |
Therefore, by setting
![]() with
with
![]() gives
gives
![]() and
and
![]() , which leads
to equation 30.
, which leads
to equation 30.