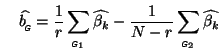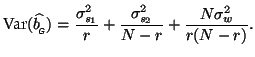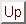

Next: Numerical simulation
Up: Examples
Previous: Numerical simulation
We assume that the individual
subjects are grouped in two groups and that within each group the
first-level parameters are normally distributed around a
group-specific mean. That is
and
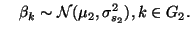
In order to simplify further notation and without loss of generality
we assume that the subjects 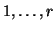 belong to the first group and
subjects
belong to the first group and
subjects
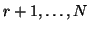 belong to the second group. We do not make any
assumption about the first-level covariance structure and simply set
belong to the second group. We do not make any
assumption about the first-level covariance structure and simply set
Then
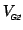 is block diagonal with elements
is block diagonal with elements
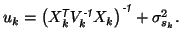 If we define
If we define
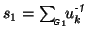 and
and
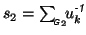 , the group parameter estimate writes as
, the group parameter estimate writes as
where the variance, as usual, is calculated from the first term as
Under the same assumptions as before, of equal covariance at
the first level and normalised designs (i.e. homoscedastic model),
these equation simplify to
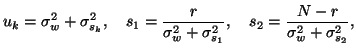
and thus
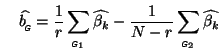
with
Note that the second level contrast includes an appropriate scaling
constant. This factor becomes irrelevant once the group parameter of
interest is combined with its variance to form a test statistic.
Subsections


Next: Numerical simulation
Up: Examples
Previous: Numerical simulation
Christian Beckmann
2003-07-16
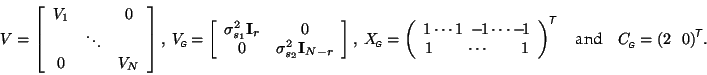
![]() is block diagonal with elements
is block diagonal with elements
![]() If we define
If we define
![]() and
and
![]() , the group parameter estimate writes as
, the group parameter estimate writes as
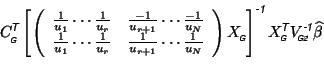
![\begin{displaymath}\!\!\!\frac{C_{_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}}^{\m...
...}}}}}_2}\!\!\frac{\widehat{\beta_k}}{u_k}\\
\end{array}\right]\end{displaymath}](img158.png)
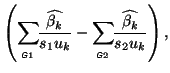
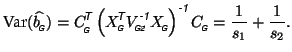
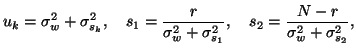 and thus
and thus