Artificial signal in synthetic noise

Figure 5: Spatio-temporal accuracy of different exploratory data analysis techniques on artificial FMRI data (10 artificial signals embedded in 180-dimensional Gaussian noise as described in section 5): (i) correlation structure of the time courses of the 10 sources; (ii)-(iv) correlation structure of time courses estimated using PICA, PCA and FDA respectively; (v) eigenspectrum of the data together with different estimators for the number of sources at ; (vi)-(viii) ROC curves: false-positives rate (0-0.12) vs. true- positives rate (0.4-1) for the estimated spatial maps, markers indicate the results for the canonical threshold level $0.5$.

This data set approximately conforms to the model assumptions from equation 2 and is used here to illustrate the difference between a PICA decomposition and results from standard PCA and regularised PCA, or functional data analysis. FDA was carried out as described in [Ramsay and Silverman, 1997] using a set of 60 $B$-spline basis functions.

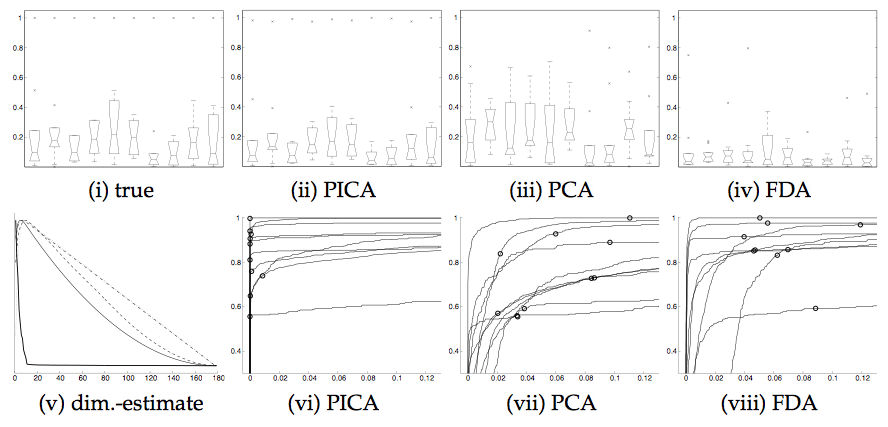
Figure 5 summarises the spatio-temporal accuracy of the decompositions for all three techniques. For both FDA and PCA, the first 10 estimated sources were chosen for the comparison; in the case of PICA the model selection correctly identifies the number true number of hidden sources (figure 5), so only 10 source signals are estimated. The top row shows boxplots of the cross-correlation between the 10 true and the 10 estimated time courses (i.e. the first boxplot summarises the temporal cross-correlation between source nr. 1 and all other time courses) while the bottom row shows ROC curves for each of the 10 associated spatial maps. For both PCA and FDA, the estimated time courses differ substantially from the 'true' time courses. While in almost all cases both techniques estimate at least one time course with a significant correlation, the overall correlation structure is not preserved (figure 5 (i) compared to (iii) and (iv)) . This is a simple consequence of the fact that both PCA and FDA estimate orthogonal sets of time courses. Note that FDA appears to perform worse in terms of the estimation of the time courses but outperforms PCA in the spatial domain. In the case of PICA, the underlying sources are much better identified, both in the temporal and the spatial domain: the correlation structure of the estimated time courses is close to that of the true source signals. At the same time the PICA decomposition results in an improved ROC characteristics with highest true-positive rates at any false- positives level. In almost all cases the canonical threshold level of 0.5 results in 0 false positives. In this case, the difference between PICA and PCA is purely due to the additional orthogonal rotation matrix $Q$. In the case of PICA the underlying sources are much better identified in that in all cases exactly one of the estimated time courses has a very high correlation with the true signal time course. Consequently, the covariance structure between different time courses is almost identical to the true covariance structure. It is interesting to note that, in all cases, the estimated time courses have a slightly smaller cross-covariance structure than the true time courses. This is an effect quite different to the assumptions that lead into the investigation of 'Spatiotemporal Independent Component Analysis' [Stone et al., 2002] . There, the authors speculated that in in the case of an ICA decomposition based on optimising spatial independence between estimated source signals, suboptimal solutions emerge since the decomposition will tend towards unplausible solutions in the 'dual' temporal domain in order to satisfy the independence in the spatial domain. In our experience, however, spatial and temporal accuracy appear to be strongly related. This is, in fact, what is to be expected given the uniqueness results presented earlier.