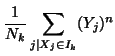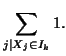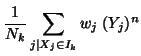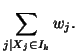

Next: Joint Histogram Apodization
Up: Methods
Previous: Methods
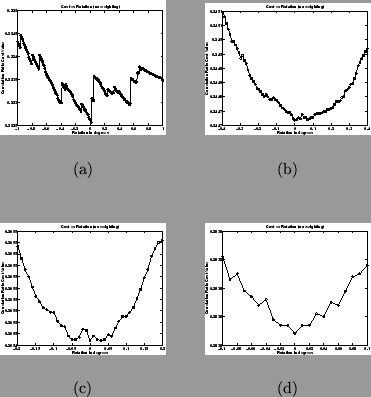
As seen in Figure 1, the local behaviour of the cost
function shows small discontinuities as the transformation parameters
are varied smoothly. This creates local minima ``traps'' for the
optimisation method. Since all interpolation methods are continuous
(except nearest neighbour which is consequently seldom used) the
discontinuities are not due to the type of interpolation used. The
cause of these discontinuities is the changing amount of
overlap of the reference and floating image.
Figure 1:
Plots of the Correlation Ratio cost function versus rotation
about the 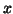 -axis, showing the presence of local discontinuities.
Such discontinuities can sometimes signify the presence of local
minima. The resolution of the images are: (a) 8mm, (b) 4mm, (c) 2mm
and (d) 1mm. Note that the range of angles shown and the size of
discontinuity decreases as the resolution scale decreases. Therefore
the problem is greater at larger scales. Note that each individual
sample of the cost function is denoted by a circle.
-axis, showing the presence of local discontinuities.
Such discontinuities can sometimes signify the presence of local
minima. The resolution of the images are: (a) 8mm, (b) 4mm, (c) 2mm
and (d) 1mm. Note that the range of angles shown and the size of
discontinuity decreases as the resolution scale decreases. Therefore
the problem is greater at larger scales. Note that each individual
sample of the cost function is denoted by a circle.
 |
There are two different ways of treating values outside the Field of
View (FOV) of an image:
- Treat all values outside the FOV as zero.
- Do all calculations strictly in the overlapping region.
The first method is undesirable as it creates artificial intensity
boundaries when the object is not wholly contained within the FOV.
However, in the second method the number of points counted in the
overlapping region varies, not just the expressions involving
intensities. Therefore, in the second case both the numerator and
denominator of the cost functions (except Least Squares) will change
discontinuously as the amount of overlap changes.
The discontinuities exist because the images are discrete sets of
voxels. In particular, the reference image defines a fixed set of
voxel locations over which the cost function is calculated. Then, for
a given transformation, the floating image intensities at these
locations are calculated using interpolation. A reference image voxel
location is only counted when it is valid: that is, within the
overlapping region such that it maps to a location inside the FOV of
the floating image. When the edge of the FOV of the floating image
crosses a reference voxel location, the location suddenly goes from
being inside the overlapping region to outside, causing a
discontinuous change in the number of valid locations, as shown in
Figure 2.
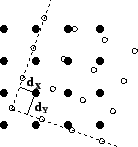
Figure 2:
Example showing how the overlapping region of
the FOV for the reference image (filled dots) and floating image (open
dots) can change with transformation. The shortest distances, 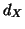 and
and 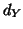 , (shown as a solid lines) to the edges of the overlapping
region (shown by the dashed lines) are illustrated for a single
reference voxel location.
, (shown as a solid lines) to the edges of the overlapping
region (shown by the dashed lines) are illustrated for a single
reference voxel location.
 |
We aim to apodize the cost function by removing these
discontinuities. To do this, our approach has been to introduce a
geometric apodization that de-weights the contributions of
locations that are near the edge of the overlapping region. The
weighting is chosen so that the contribution of such locations drops
continuously until it reaches zero at the edge of the overlapping
region. Any continuous weighting function could be used but for
simplicity and computational efficiency we choose one that is linear.
For instance, consider a 2D example of a reference location that maps
to a point inside the overlapping region, where the distance from the
nearest edges of the floating image FOV are 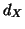 and
and 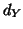 units, as
shown in Figure 2. In each dimension, if this
value is less than some threshold
units, as
shown in Figure 2. In each dimension, if this
value is less than some threshold 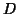 , then the influence of that
point is weighted by a weight
, then the influence of that
point is weighted by a weight 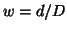 . In higher dimensions, the
product of the weighting functions in each dimension is used. That is:
. In higher dimensions, the
product of the weighting functions in each dimension is used. That is:
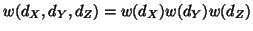 .
The weighting is applied to all terms involving that location's
intensity as well as to the number of locations in the region. For
example, consider the
.
The weighting is applied to all terms involving that location's
intensity as well as to the number of locations in the region. For
example, consider the 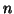 th moment of an iso-set:
th moment of an iso-set:
where 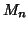 is the
is the 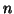 th moment,
th moment, 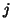 is a voxel index,
is a voxel index, 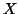 and
and 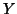 represent the reference and floating images respectively and
represent the reference and floating images respectively and 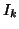 denotes the
denotes the 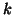 th intensity bin. With general weighting this becomes:
th intensity bin. With general weighting this becomes:
where 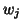 is the weight of the location
is the weight of the location 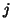 , which is
0 outside the overlapping region,
, which is
0 outside the overlapping region, 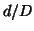 for
for 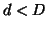 or 1 for
or 1 for 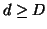 inside
the overlapping region.
This weighting scheme can be simply and efficiently applied to any of
the non entropy-based cost functions (i.e. LS, NC, W and CR). It
depends on one parameter -- the threshold distance
inside
the overlapping region.
This weighting scheme can be simply and efficiently applied to any of
the non entropy-based cost functions (i.e. LS, NC, W and CR). It
depends on one parameter -- the threshold distance 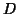 -- which can
be varied to increase the amount of apodization. When
-- which can
be varied to increase the amount of apodization. When 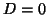 there
is no apodization, whilst increasing
there
is no apodization, whilst increasing 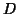 creates smoother and
smoother cost functions, although the cost function will be continuous
for any non-zero value of
creates smoother and
smoother cost functions, although the cost function will be continuous
for any non-zero value of 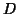 . Also note that making
. Also note that making 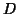 larger than the voxel spacing is permitted and just has a greater
smoothing effect, as shown in Figure 3.
larger than the voxel spacing is permitted and just has a greater
smoothing effect, as shown in Figure 3.
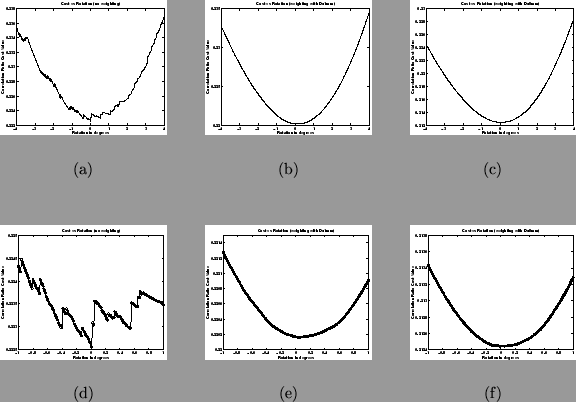
Figure 3:
Plots of the
Correlation Ratio cost function versus rotation at different values
for the geometric apodization threshold, 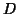 . The values of
. The values of 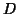 shown
are 0mm, 1mm and 8mm for the three columns (left to right
respectively). The resolution in each case is 8mm and the bottom row
shows the same values over an expanded scale. Each plot was generated
by measuring the cost functions between two real images, about the
estimate of the global minimum, which was a non-identity
transformation and so did not correspond to maximum overlap of the
FOVs. This clearly shows that the apodization has the desired
smoothing effect on the cost function, eliminating large
discontinuities. Note that each individual sample of the cost
function in the bottom row is denoted by a circle.
shown
are 0mm, 1mm and 8mm for the three columns (left to right
respectively). The resolution in each case is 8mm and the bottom row
shows the same values over an expanded scale. Each plot was generated
by measuring the cost functions between two real images, about the
estimate of the global minimum, which was a non-identity
transformation and so did not correspond to maximum overlap of the
FOVs. This clearly shows that the apodization has the desired
smoothing effect on the cost function, eliminating large
discontinuities. Note that each individual sample of the cost
function in the bottom row is denoted by a circle.
 |
Subsections


Next: Joint Histogram Apodization
Up: Methods
Previous: Methods
Peter Bannister
2002-05-03