

Next: A Global-Local Hybrid Optimisation
Up: Apodization of the Cost
Previous: Apodization of the Cost
A more general weighting scheme is required for apodizing the joint
histogram required for the entropy-based cost functions. This is
because the number of entries in each histogram bin becomes
discontinuous as the intensity at a floating image location
(calculated using interpolation) passes through the threshold value
between intensity bins.
As it is the intensity passing through a threshold value that causes
the discontinuities for the joint histogram, we propose a weighting
function that is determined by the intensities and applied to every
location. We choose, once again, a linear weighting function (as
shown in Figure 4) where 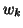 is the weight for bin
is the weight for bin
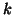 ,
, 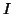 is the intensity at the location under consideration,
is the intensity at the location under consideration, 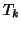 is the intensity threshold between bins
is the intensity threshold between bins 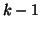 and
and 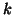 , and
, and 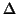 is
the smoothing threshold -- the equivalent of
is
the smoothing threshold -- the equivalent of 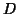 in the preceding
section. This weight is then applied to the accumulation of intensity
within the joint histogram bin, as well as the number of entries in
the bin, which is no longer an integer. That is for a point of
intensity
in the preceding
section. This weight is then applied to the accumulation of intensity
within the joint histogram bin, as well as the number of entries in
the bin, which is no longer an integer. That is for a point of
intensity 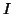 , the updating equations for bin
, the updating equations for bin 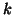 are:
are:
where
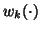 is the weighting function for the
is the weighting function for the 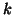 th bin (see figure 4),
th bin (see figure 4), 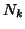 is the occupancy of bin
is the occupancy of bin 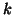 (a non-integer version of
the number of elements), and
(a non-integer version of
the number of elements), and 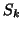 is the sum of intensities in the bin.
is the sum of intensities in the bin.
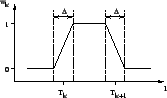
Figure 4:
Weighting function used for
apodization of the entropy-based cost functions. This weighting
function is equivalent to a fuzzy-bin membership function based on the
intensity 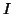 .
.
 |
This approach is effectively fuzzy-binning, where each intensity bin
no longer has sharp thresholds, but fuzzy membership functions. It
also means that a given location can influence more than one bin
entry. Because of the way the weighting function is calculated
though, each location contributes equally, since the sum of weights
for all bin entries is equal to one.
As changing overlap will still create discontinuities, both the
geometrical weighting and the fuzzy-binning need to be applied to have
a continuous joint histogram. Moreover, the parameter 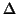 will
give a continuous joint histogram for any value greater than zero,
although the value should not exceed the intensity bin width. The
smoothing capacity of
will
give a continuous joint histogram for any value greater than zero,
although the value should not exceed the intensity bin width. The
smoothing capacity of 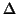 is shown in Figure 5
for the Mutual Information cost function. Results for the Normalised
Mutual Information cost function are very similar. Note that, in
general, a value of
is shown in Figure 5
for the Mutual Information cost function. Results for the Normalised
Mutual Information cost function are very similar. Note that, in
general, a value of
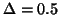 together with
together with 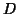 equal to the resolution
scale (e.g. 8mm), gives a desirably smooth cost function.
Note that the Partial Volume Interpolation introduced by
Maes [13] also creates continuous joint histogram estimates
if used in conjunction with the geometrical weighting (applied to the
reference locations instead). However, as the name suggests, PVI is
more than just a apodization scheme -- in fact it functions as an
interpolation method too. Therefore, different interpolation methods
cannot be used in conjunction with PVI, whereas for fuzzy-binning the
interpolation method used can be freely chosen. Furthermore, the
fuzzy-binning scheme provides an adjustable parameter,
equal to the resolution
scale (e.g. 8mm), gives a desirably smooth cost function.
Note that the Partial Volume Interpolation introduced by
Maes [13] also creates continuous joint histogram estimates
if used in conjunction with the geometrical weighting (applied to the
reference locations instead). However, as the name suggests, PVI is
more than just a apodization scheme -- in fact it functions as an
interpolation method too. Therefore, different interpolation methods
cannot be used in conjunction with PVI, whereas for fuzzy-binning the
interpolation method used can be freely chosen. Furthermore, the
fuzzy-binning scheme provides an adjustable parameter, 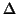 , which
controls the amount of smoothing of the cost function, allowing for
different degrees of smoothing, as desired.
Finally, it can be seen that fuzzy-binning can be made fully symmetric
with respect to the two images (see [2] for a discussion
of symmetry in general registration cost functions). That is, both
floating and reference intensities can have fuzzy-binning applied to
them. However, there is an inherent asymmetry in the way that
interpolation is applied only to the floating image. Therefore,
although such a symmetric approach appears initially attractive, the
simpler and faster approach of only using fuzzy-bins for the floating
image was adopted in practice.
, which
controls the amount of smoothing of the cost function, allowing for
different degrees of smoothing, as desired.
Finally, it can be seen that fuzzy-binning can be made fully symmetric
with respect to the two images (see [2] for a discussion
of symmetry in general registration cost functions). That is, both
floating and reference intensities can have fuzzy-binning applied to
them. However, there is an inherent asymmetry in the way that
interpolation is applied only to the floating image. Therefore,
although such a symmetric approach appears initially attractive, the
simpler and faster approach of only using fuzzy-bins for the floating
image was adopted in practice.
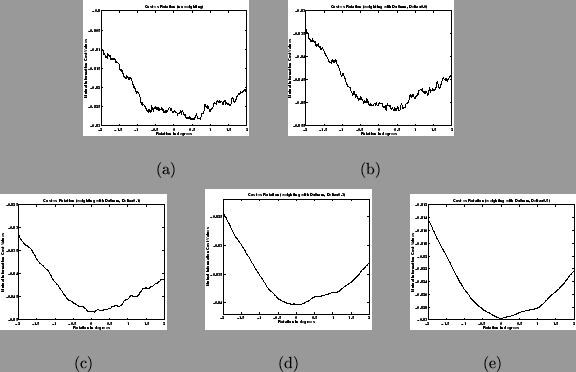
Figure 5:
Plots of the
Mutual Information cost functions versus rotation at different values
for the fuzzy-binning apodization threshold, 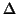 . The values of
. The values of
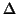 shown are 0.0 for the top row and 0.1, 0.3 and 0.5 for the
three columns (left to right respectively) in the bottom row. In (a)
no geometric apodization is applied, whilst in (b) to (e), the
geometric apodization with
shown are 0.0 for the top row and 0.1, 0.3 and 0.5 for the
three columns (left to right respectively) in the bottom row. In (a)
no geometric apodization is applied, whilst in (b) to (e), the
geometric apodization with 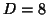 mm is applied together with
fuzzy-binning for (c) to (e). The resolution of the image in each
case is 8mm. Each plot was generated by measuring the cost functions
between two real images, about the estimate of the global minimum,
which was a non-identity transformation and so did not correspond to
maximum overlap of the FOVs. This clearly shows that both apodization
methods are required to have the desired smoothing effect on the cost
function, eliminating large discontinuities. In general, a value of
mm is applied together with
fuzzy-binning for (c) to (e). The resolution of the image in each
case is 8mm. Each plot was generated by measuring the cost functions
between two real images, about the estimate of the global minimum,
which was a non-identity transformation and so did not correspond to
maximum overlap of the FOVs. This clearly shows that both apodization
methods are required to have the desired smoothing effect on the cost
function, eliminating large discontinuities. In general, a value of
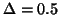 together with
together with 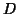 equal to the resolution scale
(e.g. 8mm), gives a desirably smooth cost function.
equal to the resolution scale
(e.g. 8mm), gives a desirably smooth cost function.
 |


Next: A Global-Local Hybrid Optimisation
Up: Apodization of the Cost
Previous: Apodization of the Cost
Peter Bannister
2002-05-03

