

Next: Comparison with Existing Methods
Up: Robustness Assessment: Registration
Previous: Robustness Assessment: Registration
For many registration problems in practice, there is no
ground truth available to evaluate the registration. This makes
the quantitative assessment of methods quite difficult.
Therefore, to test the method quantitatively, a comparative
consistency test was performed that does not require knowledge of
the actual ground truth.
The consistency test is based on comparing registrations obtained
using various different, but known, initial starting positions of a
given image. If the registrations are consistent then the final
registered image will be the same, regardless of the starting
position. Consistency is a necessary, but
not sufficient condition that all correctly functioning
registration methods must possess. This is essentially a measure of
the robustness rather than the accuracy [17] of the
registration method. Robustness is defined here as the ability to get
close to the global minimum on all trials, whereas accuracy is the
ability to precisely locate a (possibly local) minimum of the cost
function. Ideally a registration method should be both robust and
accurate.
More specifically, the consistency test for an individual image 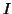 involved taking the image and applying several pre-determined affine
transformations,
involved taking the image and applying several pre-determined affine
transformations, 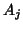 to it (with appropriate cropping so that no
`padding' of the images was required). All these images (both
transformed and un-transformed) were registered to a given reference
image,
to it (with appropriate cropping so that no
`padding' of the images was required). All these images (both
transformed and un-transformed) were registered to a given reference
image, 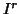 , giving transformations
, giving transformations 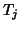 . If the method was
consistent the composite transformations
. If the method was
consistent the composite transformations
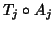 should all be
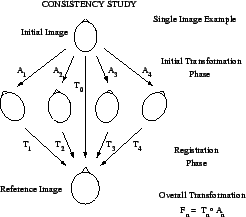
the same, as illustrated in Figure 8.
should all be
the same, as illustrated in Figure 8.
Figure 8:
Illustration of the
consistency test for a single image. An image (top) has a number of
initial affine transformations 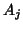 applied to it. The resulting
images (middle) are then registered to the reference image (bottom),
giving transformations
applied to it. The resulting
images (middle) are then registered to the reference image (bottom),
giving transformations 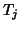 . Therefore, the overall transformation
from the initial image to the reference image is
. Therefore, the overall transformation
from the initial image to the reference image is
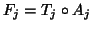 , and these are compared with
, and these are compared with 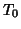 which is the registration of
the initial image directly to the reference image. For a consistent
method, all the transformations,
which is the registration of
the initial image directly to the reference image. For a consistent
method, all the transformations, 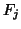 , should be the same as
, should be the same as 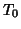 .
.
 |
The transformations are compared quantitatively using the RMS
deviation between the composite registration
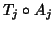 and the
registration from the un-transformed case
and the
registration from the un-transformed case 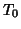 . This RMS deviation
is calculated directly from the affine
matrices [11]. That is:
. This RMS deviation
is calculated directly from the affine
matrices [11]. That is:
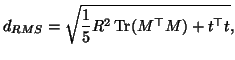 |
(6) |
where 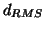 is the RMS deviation in mm,
is the RMS deviation in mm, 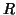 is a radius specifying the
volume of interest, and
is a radius specifying the
volume of interest, and
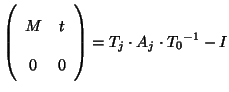 is used to
calculate the
is used to
calculate the
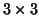 matrix
matrix 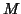 and the
and the
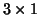 vector
vector 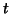 .
.


Next: Comparison with Existing Methods
Up: Robustness Assessment: Registration
Previous: Robustness Assessment: Registration
Peter Bannister
2002-05-03


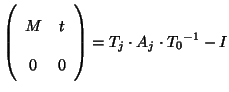 is used to
calculate the
is used to
calculate the