

Next: Interpolation
Up: Materials
Previous: Registration
Many different cost functions have been proposed for image
registration problems. Some use geometrically
defined features, found within the image, to quantify the (dis)similarity,
whilst others work directly with the intensity values in the images.
A large comparative study of different registration methods [17]
indicated that intensity-based cost functions are more accurate
and reliable than the geometrically-based ones. Consequently, most
recent registration methods have used intensity-based cost functions, and
these are the ones which will be discussed in this paper.
Intensity-based cost functions can be divided naturally into two
categories: those suitable for intra-modal problems and those suitable
for inter-modal problems. In the former category the most commonly
used cost functions are: least squares (LS) and normalised
correlation (NC). For the latter, and more difficult, category the most
commonly used functions are: mutual information (MI),
normalised mutual information (NMI), woods (W) and
correlation ratio (CR). These functions are defined mathematically
in Table 1 (see [12] for more information).
Table 1:
Mathematical definitions of the most commonly used
intensity-based cost functions: Least Squares (LS); Normalised
Correlation (NC); Woods (W); Correlation
Ratio (CR); Mutual Information (MI); and Normalised Mutual Information
(NMI). The notation is: quantities 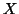 and
and 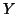 denote images, each
represented as a set of intensities;
denote images, each
represented as a set of intensities; 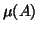 is the mean of set
is the mean of set 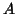 ;
;
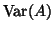 is the variance of the set
is the variance of the set 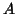 ;
; 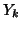 is the
is the 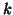 th iso-set
defined as the set of intensities in image
th iso-set
defined as the set of intensities in image 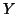 at positions where the
intensity in
at positions where the
intensity in 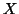 is in the
is in the 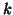 th intensity bin;
th intensity bin; 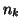 is the number of
elements in the set
is the number of
elements in the set 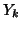 such that
such that
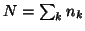 ;
;
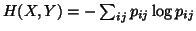 is the standard entropy definition where
is the standard entropy definition where
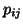 represents the probability estimated using the
represents the probability estimated using the 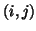 joint
histogram bin, and similarly for the marginals,
joint
histogram bin, and similarly for the marginals, 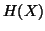 and
and 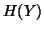 .
Note that the sums in the first two rows are taken over all
corresponding voxels.
.
Note that the sums in the first two rows are taken over all
corresponding voxels.
 |
Subsections


Next: Interpolation
Up: Materials
Previous: Registration
Peter Bannister
2002-05-03

