

Next: Point estimate of
Up: Fast Approximation Point Estimates
Previous: Fast Approximation Point Estimates
We get a point estimate of
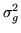 by finding the maximum a
posterior (MAP) over the marginal posterior distribution
by finding the maximum a
posterior (MAP) over the marginal posterior distribution
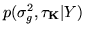 . If we marginalise out
. If we marginalise out 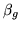 then the marginal posterior is:
then the marginal posterior is:
where
We then assume 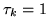 and look to find the MAP for
and look to find the MAP for
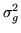 . However, there is a question of parameterisation.
The mode we get will depend on the parametrisation we use. For
example, we could look to maximise with respect to
. However, there is a question of parameterisation.
The mode we get will depend on the parametrisation we use. For
example, we could look to maximise with respect to
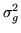 ,
or
,
or 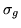 , or
, or
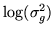 , or
, or
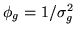 etc., all of which will give us different MAPs. Note that as we
reparameterise, the reference prior might change but the reference
posterior always stays the same, see (2). Hence, a
natural way to reparameterise such that the parameter we use gives
us a uniform reference prior.
etc., all of which will give us different MAPs. Note that as we
reparameterise, the reference prior might change but the reference
posterior always stays the same, see (2). Hence, a
natural way to reparameterise such that the parameter we use gives
us a uniform reference prior.
The parameterisation which gives us a uniform reference prior is
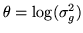 . Hence, we need to solve:
. Hence, we need to solve:
where
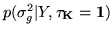 is the marginal in
equation 43 with
is the marginal in
equation 43 with
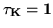 . To solve for
. To solve for
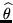 using this equation we use Brent's
algorithm (3). We can then easily convert from
using this equation we use Brent's
algorithm (3). We can then easily convert from
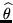 to
to
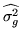 .
.


Next: Point estimate of
Up: Fast Approximation Point Estimates
Previous: Fast Approximation Point Estimates
![]() by finding the maximum a
posterior (MAP) over the marginal posterior distribution
by finding the maximum a
posterior (MAP) over the marginal posterior distribution
![]() . If we marginalise out
. If we marginalise out ![]() then the marginal posterior is:
then the marginal posterior is:
![]() . Hence, we need to solve:
. Hence, we need to solve: