

Next: Bibliography
Up: Fast Approximation Point Estimates
Previous: Point estimate of
We approximate
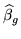 using the point estimate
using the point estimate
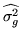 and
and
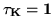 :
:
where
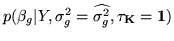 is
equation 15 with
is
equation 15 with
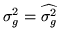 and
and
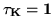 . The
solution to this is:
. The
solution to this is:
with 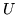 as in equation 15, but with
as in equation 15, but with
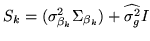 .
.
![]() using the point estimate
using the point estimate
![]() and
and
![]() :
: