Now there are two terms to be calculated. Firstly,
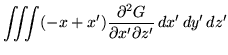 |
|||
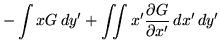 |
|||
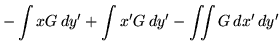 |
|||
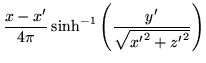 |
|||
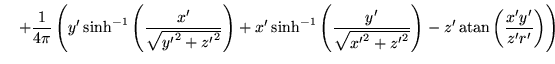 |
|||
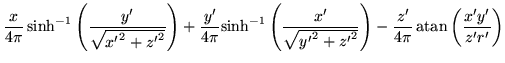 |
(32) |
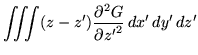 |
|||
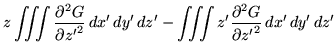 |
|||
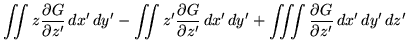 |
|||
 |
|||
 |
|||
 |
|||
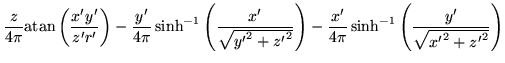 |
(33) |
Due to the linearity of equations 14 and 21 these
two terms can be combined at this stage to give
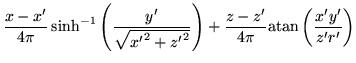 |
(34) |
Note that for ![]() and
and ![]() here both primed and
unprimed coordinates appear, whereas for the constant fields
the unprimed coordinates did not appear in the expressions for
here both primed and
unprimed coordinates appear, whereas for the constant fields
the unprimed coordinates did not appear in the expressions for ![]() .
.