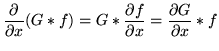Assuming the object is non-conductive (so ![]() ), the relevant
Maxwell's equations are
), the relevant
Maxwell's equations are
| 0 | (1) | ||
| 0 | (2) |
| (3) |
These equations can be reduced to a single equation by using the
magnetic scalar potential [8]
![]() .
This gives
.
This gives
Let the susceptibility, ![]() , be expanded as
, be expanded as
| (5) |
Similarly, expand ![]() in a series
in a series
| (6) |
This perturbation expansion in ![]() can be substituted back into
equation 4 to give
can be substituted back into
equation 4 to give
Using the zeroth order equation together with standard vector calculus identities gives a 3D Poisson equation
| (9) |
The Green's function for this equation is
| (10) |
From this the ![]() -component of the
-component of the ![]() field can be written as
field can be written as
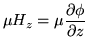 |
(12) | ||
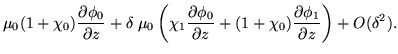 |
As the zeroth order term is
![]() , then the first order term is
, then the first order term is
Using the fact that