Equation 14 allows the first order ![]() field to be
calculated if the zeroth order field
field to be
calculated if the zeroth order field ![]() and the susceptibility
distribution
and the susceptibility
distribution ![]() are known. The zeroth order field represents the
field which would be present if there were no object in the scanner
(e.g. constant field in the
are known. The zeroth order field represents the
field which would be present if there were no object in the scanner
(e.g. constant field in the ![]() direction).
direction).
The susceptibility distribution represents the object in the scanner and needs to be specified at each point in space. For complicated functions though, the required convolutions are difficult, if not impossible, to do analytically. For most purposes, however, it is sufficient to approximate the object using small rectangular volume elements (voxels). The advantage of this is that the convolution can be done analytically for a single voxel.
Consider a single voxel of dimensions ![]() , and without loss of
generality, let it be centred at the origin
, and without loss of
generality, let it be centred at the origin ![]() with a
susceptibility of
with a
susceptibility of
![]() within the voxel and
within the voxel and
![]() outside
the voxel. Given this, the required convolutions in
equation 14 can be written as
outside
the voxel. Given this, the required convolutions in
equation 14 can be written as
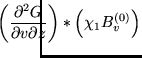 |
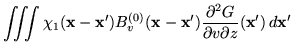 |
||
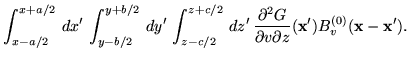 |
(19) |
The last integral can be easily calculated from the indefinite
integral, which we will denote here as
![]() . That is
. That is
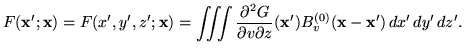 |
(20) |