As long as the null parameters are associated with areas of no interest, then they can be assigned a flat prior and integrated as shown in the previous section. However, when a shape of interest moves out of the field of view and its parameters become null parameters, then this requires special attention as the prior is no longer separable into null and non-null terms.
Specifically, consider the prior term,
![]() , and rewrite the prior as:
, and rewrite the prior as:
![$\displaystyle \alpha = \left[ \begin{array}{c} \alpha_{in} \\ \alpha_{null} \en...
... Q_{cross}^{\mathrm{\textsf{T}}}\\ Q_{cross} & & Q_{null} \end{array} \right].
$](img209.png)
This gives
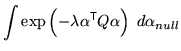 |
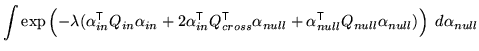 |
||
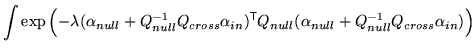 |
|||
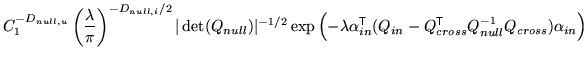 |
The resulting form is still a multi-variate Gaussian, and the effect
on the previous formula is to modify ![]() by replacing it with its
reduced form,
by replacing it with its
reduced form,
![]() and to pre-multiply the
posterior by the factor
and to pre-multiply the
posterior by the factor
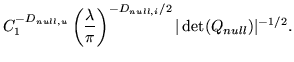
Note that because the null space of ![]() depends on both the underlying
shape models,
depends on both the underlying
shape models, ![]() , and the transformation,
, and the transformation, ![]() , both
, both ![]() and
and
![]() depend on these and so this factor will not be a constant in the
similarity function.
depend on these and so this factor will not be a constant in the
similarity function.
The posterior is now in the form
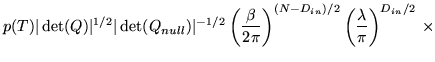 |
|||
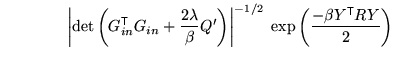 |
![$ R = I - G_{in} \left[G_{in}^{\mathrm{\textsf{T}}}
G_{in} + \frac{2\lambda}{\beta} Q'\right]^{-1} G_{in}^{\mathrm{\textsf{T}}}$](img225.png) .
.
The factor depending on ![]() does not appear, as it is cancelled by the
prior,
does not appear, as it is cancelled by the
prior,
![]() , and the normalisation of
the prior
, and the normalisation of
the prior
![]() includes
includes
![]() which cancels the other term.
which cancels the other term.