Multi-Variate Gaussian Intensity Prior

Using the Gaussian prior for the parameters of interest, $\alpha_{in}$

$$p(\alpha_{in} \vert \lambda, Q) = \vert\det(Q)\vert^{1/2} \left(\... .../2} \exp\left( - \lambda \alpha_{in}^{\mathrm{\textsf{T}}}Q \alpha_{in} \right)$$

using an inverse covariance matrix, $Q$, of dimension $D_{in}$ by $D_{in}$.

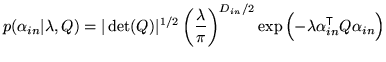Neglecting all but the interesting parameters (for now) gives a posterior of the form

$$p(T\vert Y,S,Q) \propto \int p(Y\vert T,S,\beta,\alpha) p(T) p(\alpha \vert \lambda, Q) p(\lambda) p(\sigma) \, d\sigma \, d\lambda \, d\alpha$$

$$\propto p(T) \int \left( \frac{\beta}{2 \pi} \right)^{N/2} \exp\left( \fr... ...p(\alpha \vert \lambda, Q) p(\lambda) p(\beta) \, d\beta \, d\lambda \, d\alpha$$

$$\propto p(T) \int \left( \frac{\beta}{2 \pi} \right)^{N/2} \exp\left( \fr... ...Q \alpha_{in} \right) C_0 \frac{1}{\beta} \, d\beta \, d\lambda \, d\alpha_{in}$$

$$\propto p(T) \vert\det(Q)\vert^{1/2} C_0 \int \left( \frac{\beta}{2 \pi} ... ...T}}}Q \alpha_{in} \right) \frac{1}{\beta} \, d\beta \, d\lambda \, d\alpha_{in}$$

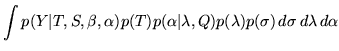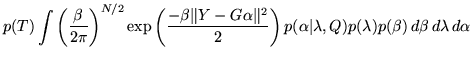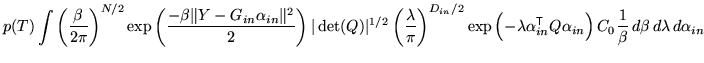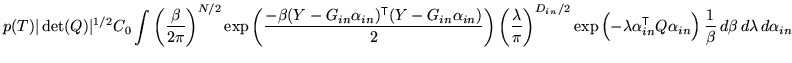When $Q \ne 0$ then the part of the posterior that depends on $\alpha_{in}$ can be written as

$$\int \exp\left( \frac{-\beta}{2} (Y- G_{in} \alpha_{in})^{\mathrm... ... \lambda \alpha_{in}^{\mathrm{\textsf{T}}}Q \alpha_{in} \right) \, d\alpha_{in}$$

$$\qquad \qquad = \int \exp\left( \frac{-\beta}{2} (Y^{\mathrm{\tex... ... \lambda \alpha_{in}^{\mathrm{\textsf{T}}}Q \alpha_{in} \right) \, d\alpha_{in}$$

$$\qquad \qquad = \int \exp\left( - (\alpha_{in}^{\mathrm{\textsf{T}}}A_1 \alpha_{in} + 2 A_2 \alpha_{in} + A_3) \right) \, d\alpha_{in}$$

$$\qquad \qquad = \left(\pi\right)^{D_{in}/2} \vert\det(A_1)\vert^{-1/2} \exp\left( A_2 A_1^{-1} A_2^{\mathrm{\textsf{T}}}- A_3 \right)$$

$$\qquad \qquad = \left(\pi\right)^{D_{in}/2} \left\vert\det\left(\... ..._{in}^{\mathrm{\textsf{T}}}Y - \frac{\beta}{2} Y^{\mathrm{\textsf{T}}}Y \right)$$

$$\qquad \qquad = \left(\frac{\beta}{2\pi}\right)^{-D_{in}/2} \left... ...t\vert^{-1/2} \; \exp\left( \frac{-\beta Y^{\mathrm{\textsf{T}}}R Y}{2} \right)$$

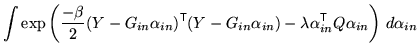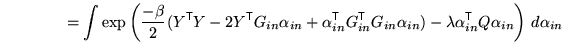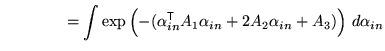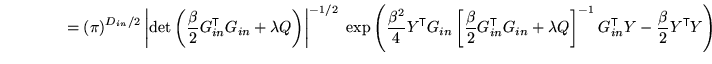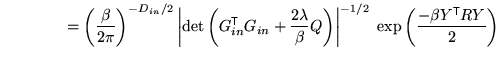where $A_1 = \frac{\beta}{2} G_{in}^{\mathrm{\textsf{T}}}G_{in} + \lambda Q$, $A_2 = - \, \frac{\beta}{2} Y^{\mathrm{\textsf{T}}}G_{in}$, $A_3 = \frac{\beta}{2} Y^{\mathrm{\textsf{T}}}Y$ and $R = I - G_{in} \left[G_{in}^{\mathrm{\textsf{T}}} G_{in} + \frac{2\lambda}{\beta} Q\right]^{-1} G_{in}^{\mathrm{\textsf{T}}}$ which is a residual forming matrix (no longer a projection matrix) and it also depends on $\beta$ and $\lambda$.

The full posterior is then

$$p(T\vert Y,S,Q,\beta,\lambda) \propto p(T) \vert\det(Q)\vert^{1/2} \left( \frac{\beta}{2 \pi} \right)^{... ...t\vert^{-1/2} \; \exp\left( \frac{-\beta Y^{\mathrm{\textsf{T}}}R Y}{2} \right)$$

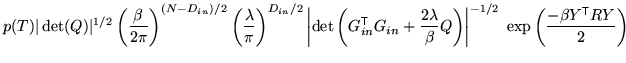This form is extremely difficult (probably impossible) to integrate analytically with respect to $\beta$ and $\lambda$. Hence it is left in this semi-marginalised form.