Marginalisation over voxels wholly in the areas of no interest
proceeds exactly as in the case of a flat intensity prior, since the
multi-variate prior here does not include these parameters. These
parameters therefore split into null, degenerate, and uninteresting.
The degenerate and uninteresting parameters integrate in the same way
as for the flat prior case and the null parameters integrate as part
of
![]() in the previous section.
in the previous section.
Specifically, this gives
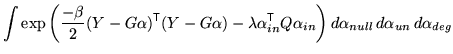 |
|||
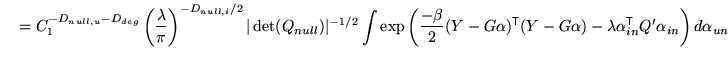 |
|||
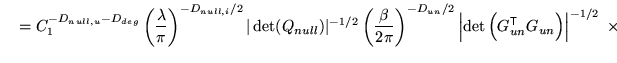 |
|||
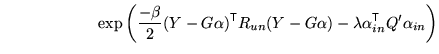 |
(10) |
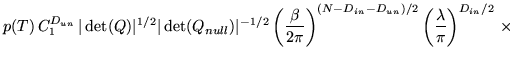 |
|||
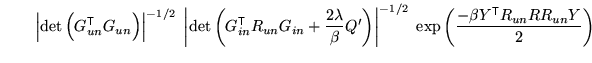 |
![$ R = I -
R_{un} G_{in} \left[G_{in}^{\mathrm{\textsf{T}}}R_{un} G_{in} + \frac{2\lambda}{\beta}
Q'\right]^{-1} G_{in}^{\mathrm{\textsf{T}}}R_{un}$](img236.png) .
.