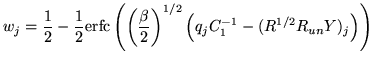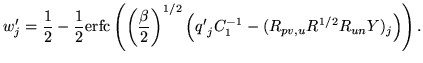Pure partial volume parameters can again be split into those
associated with shapes of interest,
![]() , and those
associated with areas of no interest,
, and those
associated with areas of no interest,
![]() . The former
have non-flat priors and the latter have flat priors. Integration of
the former requires more care, as they interact with the multi-variate
prior. In order to do this, rewrite the appropriate matrices as
. The former
have non-flat priors and the latter have flat priors. Integration of
the former requires more care, as they interact with the multi-variate
prior. In order to do this, rewrite the appropriate matrices as
![$\displaystyle \alpha = \left[ \begin{array}{c} \alpha_{pv,i} \\ \alpha_{in} \\ ...
...^{\mathrm{\textsf{T}}}\\ Q_{b} & & Q_{cross} & & Q_{null} \end{array} \right].
$](img239.png)
Therefore the posterior integrations take the form
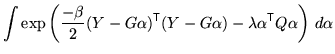 |
|||
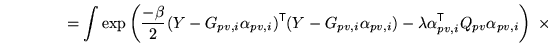 |
|||
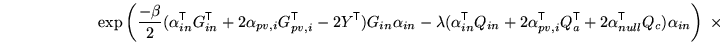 |
|||
Integrating with respect to
![]() gives
gives
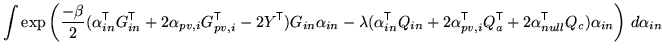 |
|||
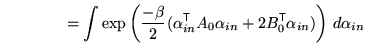 |
|||
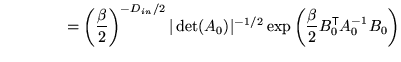 |
Substituting this back into the previous expression and integrating over
![]() gives
gives
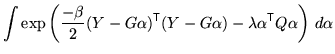 |
|||
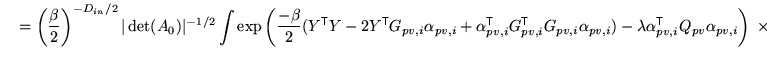 |
|||
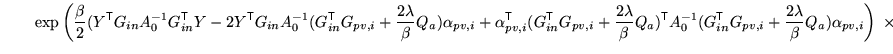 |
|||
![$\displaystyle \qquad \exp \left( - \lambda \left[ 2 Y^{\mathrm{\textsf{T}}}G_{i...
...xtsf{T}}}) \right] \alpha_{null} \right) \; \, d\alpha_{pv,i} \; d\alpha_{null}$](img251.png) |
|||
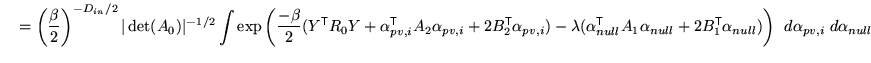 |
|||
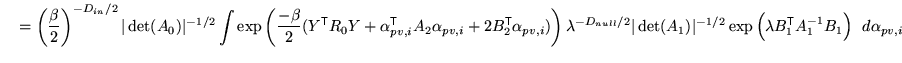 |
|||
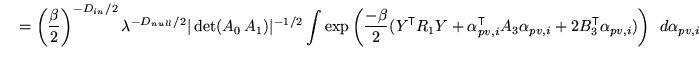 |
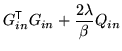 |
|||
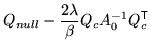 |
|||
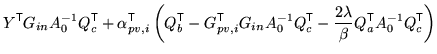 |
|||
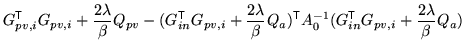 |
|||
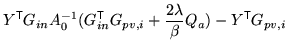 |
|||
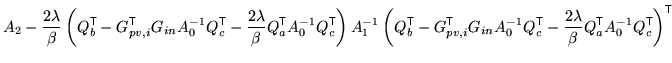 |
|||
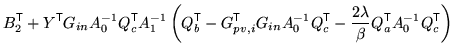 |
|||
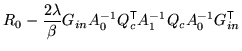 |
However, as shown above, if all the previous integrations are
performed first, then the remaining posterior takes the form
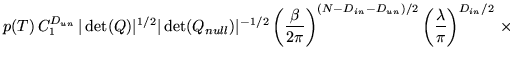 |
|||
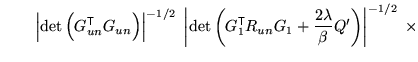 |
|||
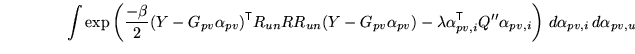 |
![$ R = I - R_{un} G_1 \left[G_1^{\mathrm{\textsf{T}}}R_{un} G_1 + \frac{2\lambda}{\beta}
Q'\right]^{-1} G_1^{\mathrm{\textsf{T}}}R_{un}$](img275.png) ;
;
![$\displaystyle Q' = \left[ \begin{array}{ccc}
Q_{pv} - Q_{b}^{\mathrm{\textsf{T...
...} - Q_{cross}^{\mathrm{\textsf{T}}}Q_{null}^{-1} Q_{cross}
\end{array} \right]
$](img277.png)
Assuming that
![]() and
and
![]() both
have negligible off-diagonal terms gives
both
have negligible off-diagonal terms gives
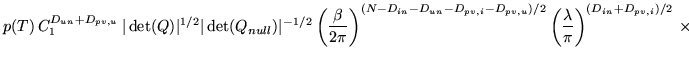 |
|||
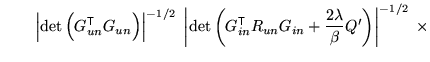 |
|||
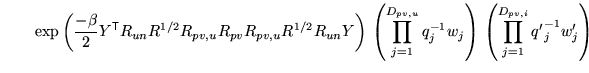 |
|||
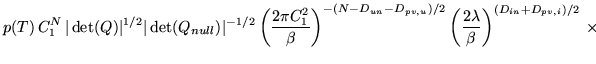 |
|||
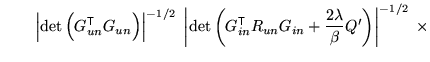 |
|||
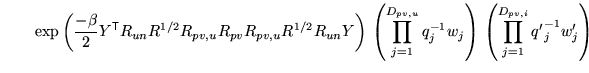 |