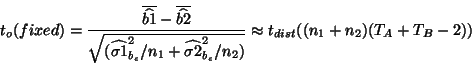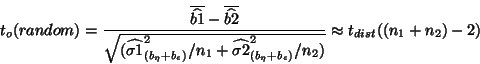Next: General Linear Model
Up: tr00dl1
Previous: Variance ratio smoothing
A one-group analysis is a multi-subjects analysis with the obvious
restriction that every subject of the random sample studied is a
member of this group.
Two-group analysis is carried out with a two-sample 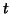 -test under the
same framework:
-test under the
same framework:
All the first level analysis has been done for every subject in
each group. Note that this looks very similar to the original
simple single-subject analysis, but here the sample size of groups
may be quite different (a situation to avoid if possible). So one
will test
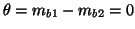 with the
statistics:7
with the
statistics:7
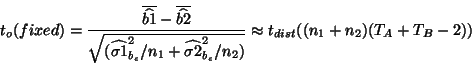 |
(12) |
or
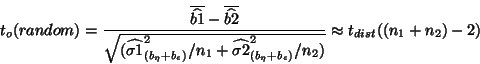 |
(13) |
with the same definitions as
in section 3 for each group. Note that here no
conjunction analysis approach can be made unless the same subjects
are in both groups (for example, before and after medical
treatment) as pairing of subjects across the groups would be
required - in fact this then ends up reverting to a one-group
analysis (with a paired 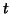 -test). The ``variance-ratio method''
can, however, be performed.
When
-test). The ``variance-ratio method''
can, however, be performed.
When  groups are studied one can compare them two by two, then
introducing a multiple comparison (not as problematic as the
statistical-map one). If equal variances are assumed, a pooled
variance of all
groups are studied one can compare them two by two, then
introducing a multiple comparison (not as problematic as the
statistical-map one). If equal variances are assumed, a pooled
variance of all  samples must be used for either method,
instead of just the two considered. To do more advanced
comparisons 8 one has to return to the GLM or ANOVA to be able to
test, for example, if all the groups have the same activation, or
if there is a trend in the groups, as one would expect for groups
defined by increasing doses of a treatment. These would involve
either F statistics and/or using a linear function of the
parameters estimated in the model, i.e. contrasts.
Remarks:
The distributions for the statistics given here are approximations
as the variance estimates are given under unequal variances
assumption and in that case the Satterthwaite formula
(3) should be used for the degrees of freedom (for the
fixed effect one has to re-integrate first levels in the formula
beforehand, see appendix). To use the degrees of freedom given one has to replace
(either in the fixed or random) the variance in each group by
their pooled
samples must be used for either method,
instead of just the two considered. To do more advanced
comparisons 8 one has to return to the GLM or ANOVA to be able to
test, for example, if all the groups have the same activation, or
if there is a trend in the groups, as one would expect for groups
defined by increasing doses of a treatment. These would involve
either F statistics and/or using a linear function of the
parameters estimated in the model, i.e. contrasts.
Remarks:
The distributions for the statistics given here are approximations
as the variance estimates are given under unequal variances
assumption and in that case the Satterthwaite formula
(3) should be used for the degrees of freedom (for the
fixed effect one has to re-integrate first levels in the formula
beforehand, see appendix). To use the degrees of freedom given one has to replace
(either in the fixed or random) the variance in each group by
their pooled
Notice that for equal sample sizes (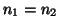 ) the pooled
estimate of the variance would give the same result for
) the pooled
estimate of the variance would give the same result for 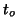 as the unequal
variance and so the given distributions become exact.
as the unequal
variance and so the given distributions become exact.



Next: General Linear Model
Up: tr00dl1
Previous: Variance ratio smoothing
Didier Leibovici
2001-03-01