


Next: Multi-subject analysis with GLM
Up: General Linear Model
Previous: Taking into account the
Introducing GLM modelling involves the choice of the ``design matrix'' 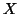 implying a model for
the observed
implying a model for
the observed 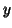 , and the choice of the covariance structure (e.g. autocorrelation pattern)
which relates to the sources of errors.
In a simple way,
, and the choice of the covariance structure (e.g. autocorrelation pattern)
which relates to the sources of errors.
In a simple way, 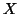 models what is expected and
models what is expected and 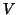 models the
errors25. What is not put in
models the
errors25. What is not put in 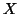 will be reflected in the errors
and may need an appropriate structure to be properly taken into
account for a ``good'' model. Inversely, what is put in
will be reflected in the errors
and may need an appropriate structure to be properly taken into
account for a ``good'' model. Inversely, what is put in 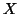 is
taken away from the errors. A good example of this is a confound
covariate which will be put into the design
is
taken away from the errors. A good example of this is a confound
covariate which will be put into the design 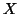 to account for in
the model as explaining what is expected, therefore adjusting the
other fixed effects and not inflating error variation otherwise.
The subject effect can be thought to be part of the model (
to account for in
the model as explaining what is expected, therefore adjusting the
other fixed effects and not inflating error variation otherwise.
The subject effect can be thought to be part of the model (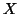 ) because one would expect different
responses for different subjects. But that way the error variation will not take into account the
sampling variation of the subjects (fixed approach), unless it is properly modelled as well in
) because one would expect different
responses for different subjects. But that way the error variation will not take into account the
sampling variation of the subjects (fixed approach), unless it is properly modelled as well in 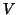 (implying random approach). Note that if one does not include the subjects in the model (
(implying random approach). Note that if one does not include the subjects in the model (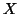 ), the
sampling variations will be considered in the errors, but will be pooled with the other sources of
errors. We will come back to these points in the next section.
The problem of GLM with structured covariance lies in the estimation
of
), the
sampling variations will be considered in the errors, but will be pooled with the other sources of
errors. We will come back to these points in the next section.
The problem of GLM with structured covariance lies in the estimation
of 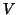 and
and 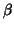 at the same time. Mixed models are GLM models of
this type where part of the covariance structure comes from random
effects. Part of the design describes fixed effects and part of it
describes random effects:
at the same time. Mixed models are GLM models of
this type where part of the covariance structure comes from random
effects. Part of the design describes fixed effects and part of it
describes random effects:
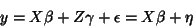 |
(28) |
with
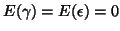 ,
,
 ,
,
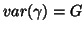 and
and
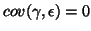 , or,
, or,
 and
and
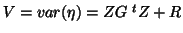 . Maximum likelihood techniques such as REML (REstricted
ML see [3] for example) find
. Maximum likelihood techniques such as REML (REstricted
ML see [3] for example) find 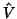 maximising
maximising
![\begin{displaymath}
\ell_R(G,R)=-\frac{1}{2}[\log\vert V\vert+ \log\vert{\;}^tX...
...rt +
{}^t(y-X\hat{\beta}_{GLS})V^{-1}(y-X\hat{\beta}_{GLS})]
\end{displaymath}](img257.gif) |
(29) |
and then plug it into the GLS estimator of
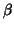 to have a final
to have a final
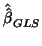 . For small samples, obtaining REML maximisation
might be unreliable in the general case and still problematic for the unequal within-subject
covariances hypothesis, but in a lot of situations the maximisation problem is simplified and can
even lead to direct calculation.
In the general case the Mixed model can accept any form for
. For small samples, obtaining REML maximisation
might be unreliable in the general case and still problematic for the unequal within-subject
covariances hypothesis, but in a lot of situations the maximisation problem is simplified and can
even lead to direct calculation.
In the general case the Mixed model can accept any form for 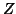 ,
,
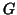 and
and  , then an algorithm [12] can give the
REML. For balanced data ``everything becomes simpler''. This is
because it implies
, then an algorithm [12] can give the
REML. For balanced data ``everything becomes simpler''. This is
because it implies
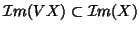 for
many situations which makes the OLS equivalent to the GLS. This is
particularly the case in fMRI (where continuous exploratory
variables come from convolution of ``balanced" dummy variables
with a model of haemodynamic response thus preserving the balanced
aspect) and that is the reason why the two-stage or two-level
approach is here valid or optimal.
Using mixed model for fMRI studies considers the random effect as the subject effect.
for
many situations which makes the OLS equivalent to the GLS. This is
particularly the case in fMRI (where continuous exploratory
variables come from convolution of ``balanced" dummy variables
with a model of haemodynamic response thus preserving the balanced
aspect) and that is the reason why the two-stage or two-level
approach is here valid or optimal.
Using mixed model for fMRI studies considers the random effect as the subject effect. 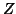 will be
a matrix of dummy variables identifying the subjects (
will be
a matrix of dummy variables identifying the subjects (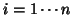 ), making
), making 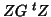 a
well-structured matrix of the form
a
well-structured matrix of the form
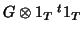 .
.  is usually
is usually
 . As the subjects are supposed to be independent
. As the subjects are supposed to be independent
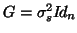 so that
so that
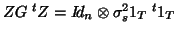 implying a constant correlation pattern for
measures within subject, it is the one used in the section 3.2.
Remark:
In this model it is important to notice introducing a pattern of
autocorrelation between time measures is not done through
implying a constant correlation pattern for
measures within subject, it is the one used in the section 3.2.
Remark:
In this model it is important to notice introducing a pattern of
autocorrelation between time measures is not done through 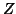 (random effects) as
(random effects) as 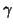 would be redundant with
would be redundant with 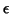 ;
it is introduced in
;
it is introduced in  .
.



Next: Multi-subject analysis with GLM
Up: General Linear Model
Previous: Taking into account the
Didier Leibovici
2001-03-01