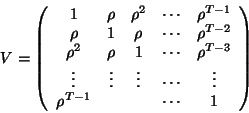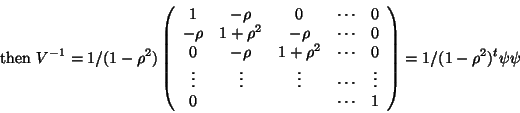Next: Applying GLM
Up: General Linear Model
Previous: Hypothesis testing and Estimability
If we suppose  one will have to estimate it. If the estimate is ``good enough'',
the estimates using GLS (sometimes called the EGLS for Estimated GLS or Empirical GLS, or plug-in
estimated or two-stage least squares) will be good as well (nearly BLUE)19. It might be difficult to obtain a good estimate (estimating
one will have to estimate it. If the estimate is ``good enough'',
the estimates using GLS (sometimes called the EGLS for Estimated GLS or Empirical GLS, or plug-in
estimated or two-stage least squares) will be good as well (nearly BLUE)19. It might be difficult to obtain a good estimate (estimating 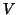 is estimating
is estimating
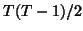 parameters), so precluding the estimated-GLS20 approach unless a model for the autocorrelation or
parameters), so precluding the estimated-GLS20 approach unless a model for the autocorrelation or 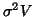 in
general can be made, reducing the number of parameters to estimate.
The pre-whitening approach is in fact the EGLS approach; usually
in
general can be made, reducing the number of parameters to estimate.
The pre-whitening approach is in fact the EGLS approach; usually 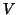 is modelled, for example, as
an autoregressive process to have fewer parameters to estimate, as in Bullmore et
al.(1996)[1]. For example let
is modelled, for example, as
an autoregressive process to have fewer parameters to estimate, as in Bullmore et
al.(1996)[1]. For example let 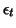 be an autoregressive process of order 1;
be an autoregressive process of order 1;
 with
with 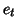 as a white noise. Then the correlation matrix
as a white noise. Then the correlation matrix 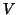 takes the form (exponential model):
takes the form (exponential model):
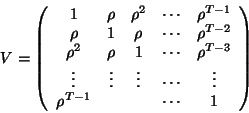 |
(23) |
where 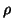 is going to be estimated, for example, on the residuals after a first stage least
squares (
is going to be estimated, for example, on the residuals after a first stage least
squares (
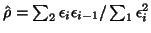 ) or by fitting an
exponential model onto the autocorrelogram. Classical time series analysis will allow estimations
for autoregressive processes with higher order of dependence.
GLS (or EGLS) uses
) or by fitting an
exponential model onto the autocorrelogram. Classical time series analysis will allow estimations
for autoregressive processes with higher order of dependence.
GLS (or EGLS) uses  and so can be very sensitive to a poor estimation of the
correlation structure. Pointing out this problem, Worsley and Friston
et.al(1995)[17] chose another way to take into account the autocorrelation. The
GLM model can be written:
and so can be very sensitive to a poor estimation of the
correlation structure. Pointing out this problem, Worsley and Friston
et.al(1995)[17] chose another way to take into account the autocorrelation. The
GLM model can be written:
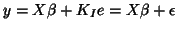 , with
, with 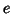 's uncorrelated, so that
's uncorrelated, so that
 . Their ``shaping approach'' uses the assumption
that their chosen matrix filtering
. Their ``shaping approach'' uses the assumption
that their chosen matrix filtering
![$K_{ij}=e^{[-(i-j)^2/2\tau^2]}$](img218.gif) (with a chosen
(with a chosen 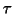 ) will
swamp the autocorrelation,
) will
swamp the autocorrelation, 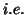
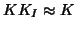 where
where  would give the true unknown one.
Under this assumption the model is then written
would give the true unknown one.
Under this assumption the model is then written
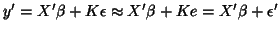 with notations
with notations 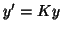 and
and  . Deriving an OLS estimate gives an
unbiased estimate but not BLUE anymore:21
. Deriving an OLS estimate gives an
unbiased estimate but not BLUE anymore:21
with variance
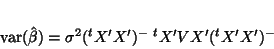 |
(24) |
given that now
 |
(25) |
To estimate 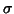 they use the same formula as described in the previous section (equation
(20) but with an OLS optimisation):
they use the same formula as described in the previous section (equation
(20) but with an OLS optimisation):
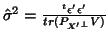 where
where
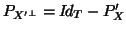 and
and
 .
The
.
The 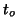 map derived in the previous section is then used with the effective degrees of
freedom22
calculated using classical results on quadratic
form theorems [12]:
map derived in the previous section is then used with the effective degrees of
freedom22
calculated using classical results on quadratic
form theorems [12]:
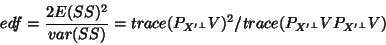 |
(26) |
The distribution of
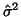 is
approximatively 23 distributed as
is
approximatively 23 distributed as 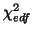 which then makes an
approximate
which then makes an
approximate 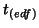 distribution for
distribution for 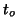 .
Notice in this presentation, without ``swamping", setting
.
Notice in this presentation, without ``swamping", setting 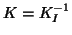 brings you back to GLS (see
previous section). Within this debate of accounting for autocorrelation in fMRI, Woolrich et al.
[16] propose a robust estimate
brings you back to GLS (see
previous section). Within this debate of accounting for autocorrelation in fMRI, Woolrich et al.
[16] propose a robust estimate  of the autocorrelation of the time
series. This robust estimate is then used either to pre-whiten the data (GLS) or to do an OLS
estimation (
of the autocorrelation of the time
series. This robust estimate is then used either to pre-whiten the data (GLS) or to do an OLS
estimation (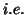 classical OLS under a non Gauss-Markov assumption24) with filtering (as in Worsley and Friston's paper but without the swamping
assumption) or without filtering (therein called variance correction) . The robustness is achieved
in two ways, firstly by smoothing the non-parametric autocorrelation function for each voxel and
secondly by smoothing the estimate spatially in a non-linear fashion to be able to preserve
different patterns according to different matter types.
Remark:
Notice that a better estimate of
classical OLS under a non Gauss-Markov assumption24) with filtering (as in Worsley and Friston's paper but without the swamping
assumption) or without filtering (therein called variance correction) . The robustness is achieved
in two ways, firstly by smoothing the non-parametric autocorrelation function for each voxel and
secondly by smoothing the estimate spatially in a non-linear fashion to be able to preserve
different patterns according to different matter types.
Remark:
Notice that a better estimate of 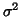 would have been using the form:
would have been using the form:
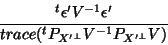 |
(27) |
as given in equation (20) (here not with the BLUE), which uses the inverse of 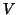 which
Worsley and Friston wanted to avoid, but this time
which
Worsley and Friston wanted to avoid, but this time 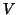 is given (Worsley and Friston) or is a
robust estimate (Woolrich et al.) It seems that having a robust estimate of
is given (Worsley and Friston) or is a
robust estimate (Woolrich et al.) It seems that having a robust estimate of 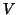 would incline one
to use a GLS approach (pre-whitening). Note that in the last version of SPM'99 (Friston et al.)
the ``swamping'' idea is dropped and an AR(1) model is used to estimate
would incline one
to use a GLS approach (pre-whitening). Note that in the last version of SPM'99 (Friston et al.)
the ``swamping'' idea is dropped and an AR(1) model is used to estimate  . As this paper is
written Friston[8] investigated the problem of estimating
. As this paper is
written Friston[8] investigated the problem of estimating  and choosing a
filter in order to minimise the bias of (24). It is known that using an unbiased
estimate
and choosing a
filter in order to minimise the bias of (24). It is known that using an unbiased
estimate  for plug-in GLS estimation (EGLS) leads to good results for point
estimation ( for
for plug-in GLS estimation (EGLS) leads to good results for point
estimation ( for 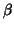 ) but to underestimation for
) but to underestimation for
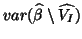 (plug-in GLS variance), and more problematic underestimation of the true variance
[2] of
(plug-in GLS variance), and more problematic underestimation of the true variance
[2] of
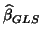 , i.e. knowing
, i.e. knowing  . So using OLS
variances with a well chosen filter and a sensible estimate of
. So using OLS
variances with a well chosen filter and a sensible estimate of  would allow to obtain a more
sensible estimate of the variance of
would allow to obtain a more
sensible estimate of the variance of
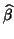 .
If
.
If  , i.e. no auto-correlation, or within the GLS framework,
, i.e. no auto-correlation, or within the GLS framework, 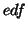 is then equal to
is then equal to
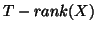 , as seen before.
, as seen before.



Next: Applying GLM
Up: General Linear Model
Previous: Hypothesis testing and Estimability
Didier Leibovici
2001-03-01