


Next: Towards Multivariable Multivariate GLM
Up: Multi-subject analysis with GLM
Previous: Random subject effect
For 2 groups or  groups this framework is used and the models are
the same. As we have already seen, to compare two groups, a
two-sample
groups this framework is used and the models are
the same. As we have already seen, to compare two groups, a
two-sample 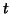 -test is used, and that will be similar here, as the use
of a contrast to compare two groups will form the difference of the
means (of the ``activation contrasts'' applied to each subject). If
one has
-test is used, and that will be similar here, as the use
of a contrast to compare two groups will form the difference of the
means (of the ``activation contrasts'' applied to each subject). If
one has  groups, multiple comparisons of pairs of groups might be
used (with some multiple comparisons corrections if needed) but an
groups, multiple comparisons of pairs of groups might be
used (with some multiple comparisons corrections if needed) but an
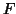 -test might be used for an overall (or more than two) group
effect.
With
-test might be used for an overall (or more than two) group
effect.
With  groups with the same number of subjects
groups with the same number of subjects 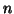 in each group,
the model will have the form:
in each group,
the model will have the form:
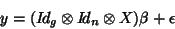 |
(41) |
with
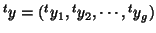 and similar for
and similar for 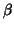 and
and 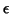 . The general
form of the ``design matrix'' would be a diagonal matrix of
. The general
form of the ``design matrix'' would be a diagonal matrix of  blocks of the form
blocks of the form
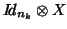 where
where  is the sample size of the
is the sample size of the 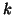 th group (notice that for the
random model when estimating the variance components the blocks are
th group (notice that for the
random model when estimating the variance components the blocks are
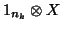 ). As the
groups are independent
). As the
groups are independent
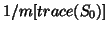 where
where 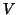 will have the form of either
the fixed or random approach in a 1 group analysis, or more generally
will have the form of either
the fixed or random approach in a 1 group analysis, or more generally
![$var(\epsilon)=diag(V_{k_{[k=1\cdots g]}})$](img335.gif) if the
if the 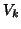 are not assumed equal or the groups are
unbalanced.
For a two-group comparison in a
are not assumed equal or the groups are
unbalanced.
For a two-group comparison in a  -group analysis, the applied
hypothesis is:
-group analysis, the applied
hypothesis is:
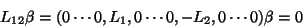 |
(42) |
where 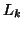 is a
is a 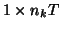 contrast, providing
the mean for this group of the activation contrast used in a
single-subject model as for a 1-group analysis. Then the
contrast, providing
the mean for this group of the activation contrast used in a
single-subject model as for a 1-group analysis. Then the 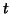 -map
is derived using the same framework as in the 1-group analysis,
using the estimates for
-map
is derived using the same framework as in the 1-group analysis,
using the estimates for 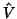 according to the approach and
the model chosen. If one wants to have a global assessment of
group differences (among more than 2 groups) the
according to the approach and
the model chosen. If one wants to have a global assessment of
group differences (among more than 2 groups) the 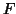 statistic
given in (22) has to be used with a contrast matrix,
statistic
given in (22) has to be used with a contrast matrix,
 to compare all the groups
to compare all the groups 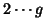 with a control group,
with a control group,
 , the matrix L of
, the matrix L of 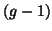 contrasts
contrasts
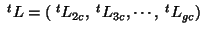 is
involved.
Remarks:
The degrees of freedom (GLS approach) to apply for
is
involved.
Remarks:
The degrees of freedom (GLS approach) to apply for 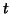 -test (2
groups comparison), for the fixed approach will be
-test (2
groups comparison), for the fixed approach will be
 , will be
, will be
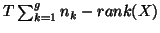 for the pooled Random and fixed model, and for the
random model with the compound symmetry covariance structure
for the pooled Random and fixed model, and for the
random model with the compound symmetry covariance structure
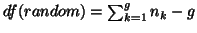 .
.



Next: Towards Multivariable Multivariate GLM
Up: Multi-subject analysis with GLM
Previous: Random subject effect
Didier Leibovici
2001-03-01