
Next: 2 and g groups
Up: Multi-subject analysis with GLM
Previous: Fixed subject effect
Firstly, notice that the random subject effect model could use this
same model with a covariance structure (block-diagonal) which would
need to be estimated in the first place. One would get a EGLS but this
model cannot be used to estimate the covariance matrix (this is
because writing this model as a mixed model makes 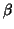 random and
fixed at the same time). One has to rewrite the model, for example
with the form:
random and
fixed at the same time). One has to rewrite the model, for example
with the form:
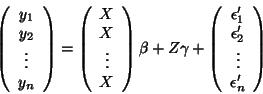 |
(35) |
or
where
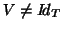 identifying the subjects (dummy variables)26 ,
with also
identifying the subjects (dummy variables)26 ,
with also 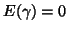 and
and 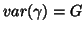 as random effects. One can easily see that OLS gives
as random effects. One can easily see that OLS gives
![$\hat{\beta}=\overline{\hat{\beta_{{(i)}}}}_{[1..n]}$](img287.gif) .
Depending on the structure of covariance chosen an estimate will be found directly (
.
Depending on the structure of covariance chosen an estimate will be found directly (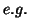 with
compound symmetry) or algorithmically (for general REML estimation). For the random analysis with
simple compound symmetry (i.e. with
with
compound symmetry) or algorithmically (for general REML estimation). For the random analysis with
simple compound symmetry (i.e. with
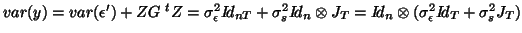 , where
, where
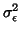 is the
scan-to-scan variation, supposed to be the same for all the subjects, and
is the
scan-to-scan variation, supposed to be the same for all the subjects, and 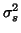 is the
random subject variation27 introducing correlations into the errors) then
with estimation for
is the
random subject variation27 introducing correlations into the errors) then
with estimation for 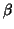 as OLS (here equivalent to GLS) ``ANOVA" estimators (equivalent to
REML) can be given by:
as OLS (here equivalent to GLS) ``ANOVA" estimators (equivalent to
REML) can be given by:
![\begin{displaymath}
\hat{\sigma}_\epsilon^2=MSE={}^tyP_{[1_n \otimes X,I\!d_n \otimes 1_T ]^\bot}y/[n(T-1) -rank(X)+1]
\end{displaymath}](img292.gif) |
(36) |
and
![\begin{displaymath}
\hat{\sigma}_s^2=\frac{MSs-MSE}{T} \mbox{ where }MSs={}^ty...
... \otimes X,I\!d_n \otimes 1_T
]}-P_{[1_n \otimes X]})y/(n-1)
\end{displaymath}](img293.gif) |
(37) |
Our interest here is only on the
subject error
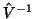 which is the two-stage approach
estimation seen before (obviously dividing by
which is the two-stage approach
estimation seen before (obviously dividing by 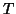 to go on second level).
to go on second level).
If all parameters in 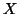 are considered as random, making
are considered as random, making
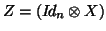 , the estimation
can be done in the same way with:
, the estimation
can be done in the same way with:
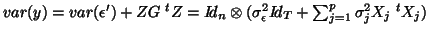 and considering the random parameters independent (non-correlated). Using Hendenson's Method
[12,3] 36 and 37 (for each random parameters) become:
and considering the random parameters independent (non-correlated). Using Hendenson's Method
[12,3] 36 and 37 (for each random parameters) become:
![\begin{displaymath}
\hat{\sigma}_\epsilon^2=MSE={}^tyP_{[1_n \otimes X,I\!d_n \otimes X]^\bot}y/[n(T-rank(X))]
\end{displaymath}](img296.gif) |
(38) |
and
![\begin{displaymath}
\hat{\sigma}_j^2=\frac{SSs -MSE {\;}(n-1)}{trace((P_{[1_n ...
...otimes X,I\!d_n \otimes X_{(-j)}]}) Id_n \otimes X_j{}^tX_j)}
\end{displaymath}](img297.gif) |
(39) |
where 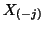 is
is 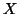 without the column
without the column 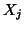 and
and
The error considered for a parameter is similarly
 ,
with
,
with
![$\theta = trace((P_{[1_n \otimes X,I\!d_n \otimes X]}-P_{[1_n
\otimes X,I\!d_n \otimes X_{(-j)}]}) Id_n \otimes X_j{}^tX_j)/(n-1)$](img302.gif) equal to
equal to 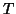 under
orthogonality of
under
orthogonality of 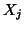 's.
For general correlation
structure, or one derived from time series analysis, instead of using an REML estimation
algorithm, a ``two-stage strategy'' could be to estimate the autocorrelation matrix
's.
For general correlation
structure, or one derived from time series analysis, instead of using an REML estimation
algorithm, a ``two-stage strategy'' could be to estimate the autocorrelation matrix 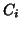 from
every subject's time series, then pool these to give an estimate of the common auto-correlation
from
every subject's time series, then pool these to give an estimate of the common auto-correlation
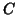 , to be able to define the covariance structure of the form
, to be able to define the covariance structure of the form
 , then solve REML (or Henderson's method III
[12]) for
, then solve REML (or Henderson's method III
[12]) for 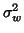 and
and 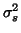 . Notice a redundancy in the previous
formula as the covariance structure describes at the same time a constant covariance for the
same subject (
. Notice a redundancy in the previous
formula as the covariance structure describes at the same time a constant covariance for the
same subject (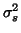 ) and the auto-covariance coming from time series autocorrelation; this
suggests a better covariance model of the form
) and the auto-covariance coming from time series autocorrelation; this
suggests a better covariance model of the form
 which then take
subject the variance component off the model (no need of
which then take
subject the variance component off the model (no need of 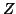 as well). At this point, time series
methods are used to estimate the
as well). At this point, time series
methods are used to estimate the 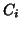 in the first place, and robust estimation such as in
Woolrich et al.[16] including the non-linear spatial smoothing would improve the
result.
in the first place, and robust estimation such as in
Woolrich et al.[16] including the non-linear spatial smoothing would improve the
result.
Remark:
The model (35) without 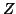 could be considered as an intermediary model (Pme) between
the fixed model (Fix) ( the model (35) but
could be considered as an intermediary model (Pme) between
the fixed model (Fix) ( the model (35) but
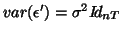 ),
i.e.
),
i.e. 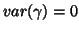 ) and the random subject model (Ran) as it can be shown that the natural
estimate of
) and the random subject model (Ran) as it can be shown that the natural
estimate of 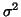 is the pooled error variance of the fixed version (
is the pooled error variance of the fixed version (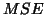 given in
(36)) of and random approaches (subject error
given in
(36)) of and random approaches (subject error  (37), but because of the
(37), but because of the 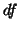 differences between the two approaches this will underestimate the error variance. This method
called here``pooling model errors" or Pme may be interesting when too few subjects are in the
study : the error variance is going to be larger than for a fixed analysis and the increase of
degrees of freedom (
differences between the two approaches this will underestimate the error variance. This method
called here``pooling model errors" or Pme may be interesting when too few subjects are in the
study : the error variance is going to be larger than for a fixed analysis and the increase of
degrees of freedom (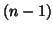 ) not too large:
) not too large:
then from model Fix ,
thereby
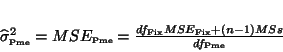 |
(40) |
and one can easily check
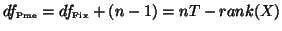 .
.


Next: 2 and g groups
Up: Multi-subject analysis with GLM
Previous: Fixed subject effect
Didier Leibovici
2001-03-01