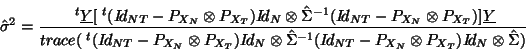Next: Discussion and Conclusions
Up: tr00dl1
Previous: 2 and g groups
Repeated-measures GLM is also available to describe fMRI studies; the so-called growth curve model
could be the best way of conceptually modelling a multi-subject experiment. It has the great
advantage of being very close to the two-stage understanding of the random subject analysis, and
of being clearly explicit for a g groups analysis.
A multivariate GLM model is usually written like the general form
we have seen before but  ,
, 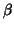 and
and 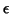 are
matrices. A multivariate linear model can be in fact rewritten as
a classical GLM and for example resolved this way as well. The
growth curve model is an extension of the multivariate GLM to
allow a model of the curve response. It is in fact also equivalent
to a classical GLM considering a tensor product of the designs:
are
matrices. A multivariate linear model can be in fact rewritten as
a classical GLM and for example resolved this way as well. The
growth curve model is an extension of the multivariate GLM to
allow a model of the curve response. It is in fact also equivalent
to a classical GLM considering a tensor product of the designs:
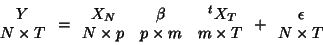 |
(43) |
For a 1-group analysis 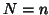 and
and 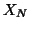 reduces to the ``constant"
reduces to the ``constant"  (or
(or 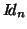 for the fixed
model), otherwise
for the fixed
model), otherwise 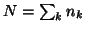 and
and 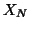 identifies the groups. Notice that
identifies the groups. Notice that  is in fact
the design we had before (then denoted
is in fact
the design we had before (then denoted 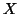 ) to identify the paradigm and covariates (within the
time series). The model (46) is in fact equivalent to the univariate model (where underlined
means all of the columns stacked,
) to identify the paradigm and covariates (within the
time series). The model (46) is in fact equivalent to the univariate model (where underlined
means all of the columns stacked, 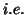
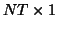 or
or 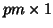 vectors)
vectors)
 |
(44) |
from which
one recognises the model (35) if one has only one group. Some algebra gives the result
for the least squares estimate:
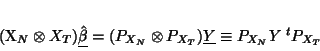 |
(45) |
(where 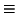 means algebraically
equivalent,
means algebraically
equivalent, 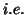 a vector
a vector 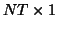 or a matrix
or a matrix 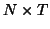 of the same thing)
28.
of the same thing)
28.
The normal distributional assumption comes with the restriction of ``separability'', 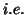 of the form
of the form
 , with usually the form
, with usually the form
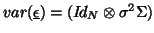 where
where 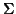 is a
is a  matrix expressing the common (to all rows) correlation of the columns (random variables) of
matrix expressing the common (to all rows) correlation of the columns (random variables) of 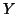 .
Historically presented by Potthof and Roy(1964) (see reference in [14]), the model
(46) was named GMANOVA (Growth curve Multivariate ANalysis Of VAriance) and was ``solved''
with a two-level analysis: projecting first according to
.
Historically presented by Potthof and Roy(1964) (see reference in [14]), the model
(46) was named GMANOVA (Growth curve Multivariate ANalysis Of VAriance) and was ``solved''
with a two-level analysis: projecting first according to  and then solving the second level
model. Let the projector onto
and then solving the second level
model. Let the projector onto  expressed with a metric
expressed with a metric 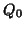 ,
,
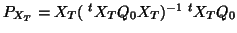 , then writing
, then writing
 one
obtains
one
obtains
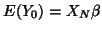 as MANOVA model. A known statistical result is that, under normality,
the least squares estimate of
as MANOVA model. A known statistical result is that, under normality,
the least squares estimate of 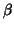 in the MANOVA model, which is in fact
in the MANOVA model, which is in fact 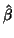 (48), is also the maximum likelihood of
(48), is also the maximum likelihood of 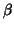 in the MANOVA model for the choice of
in the MANOVA model for the choice of
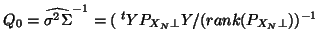 . In fMRI this
estimation is not sensible as
. In fMRI this
estimation is not sensible as  is small comparatively to
is small comparatively to 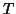 , one would prefer time series
methods (as mentioned before) to estimate the correlation structure
, one would prefer time series
methods (as mentioned before) to estimate the correlation structure 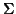 .
Estimating
.
Estimating 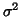 brings back to the choices between random, fixed subject analysis or the
``pooling model errors" (43). In the random analysis as in the usual Growth curve
analysis
brings back to the choices between random, fixed subject analysis or the
``pooling model errors" (43). In the random analysis as in the usual Growth curve
analysis 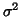 relates to common variance (across subject population) for every time
measurement, the estimate
relates to common variance (across subject population) for every time
measurement, the estimate
![$1/T [trace(Q_0)]$](img372.gif) could be used i.e. the pooling (across time) of
residual variances of the subject model (
could be used i.e. the pooling (across time) of
residual variances of the subject model (
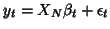 at t fixed), or could be
better estimated from the MANOVA model so with
at t fixed), or could be
better estimated from the MANOVA model so with
![$1/m [trace(S_0)]$](img374.gif) (where
(where
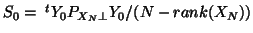 ). Notice (if
). Notice (if 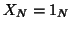 ) the diagonal of
) the diagonal of 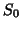 contains the variances of the parameters 29 used for
the random subject analysis (9). When
contains the variances of the parameters 29 used for
the random subject analysis (9). When 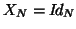 as in the fixed subject analysis, the
previous estimate does not make any sense (it is zero) and the natural estimate is used:
as in the fixed subject analysis, the
previous estimate does not make any sense (it is zero) and the natural estimate is used:
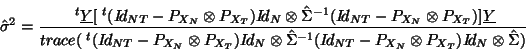 |
(46) |
with 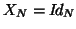 and is the pooled subject errors with autocorrelation taken into account. This
last estimate is also the ``pooling model errors" estimate of
and is the pooled subject errors with autocorrelation taken into account. This
last estimate is also the ``pooling model errors" estimate of 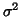 when
when
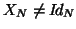 (basically
(basically  ). Model (47) could come with assumption
). Model (47) could come with assumption
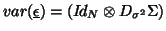 and an estimation related to the
later comment would be
and an estimation related to the
later comment would be
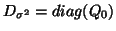 or
or
 .
To retrieve completely the mixed model, one would have to write the covariance with the form
.
To retrieve completely the mixed model, one would have to write the covariance with the form
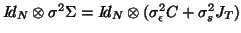 , but after
all it is not necessary in fMRI studies to split or separate the
covariance structure as the interest is only on the fixed effects
and not actually on the variance components.
The Lawley-Hotelling statistic already described (21)
can be used and a general hypothesis takes the form
, but after
all it is not necessary in fMRI studies to split or separate the
covariance structure as the interest is only on the fixed effects
and not actually on the variance components.
The Lawley-Hotelling statistic already described (21)
can be used and a general hypothesis takes the form 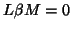 or
or
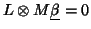 where
where 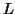 will contrast the
groups and
will contrast the
groups and 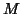 contrasts the paradigm.
Mathematically it is possible to extend further this representation
to any ``dimension'' in the data, for example incorporating the
spatial dimension:
contrasts the paradigm.
Mathematically it is possible to extend further this representation
to any ``dimension'' in the data, for example incorporating the
spatial dimension:
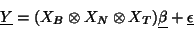 |
(47) |
where  would relate a model on the voxels (or
would relate a model on the voxels (or 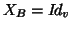 if spatial modelling is not
carried out, where
if spatial modelling is not
carried out, where 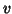 is the number of voxels),
is the number of voxels), 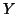 can be interpreted as a tensor of order 3
with a
can be interpreted as a tensor of order 3
with a
 vector representation. To be useful this model would have to take into
account the spatial covariance structure.
Remark:
Note that if the groups constitute a repeated experiment (
vector representation. To be useful this model would have to take into
account the spatial covariance structure.
Remark:
Note that if the groups constitute a repeated experiment (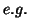 with different doses of a drug),
with different doses of a drug),
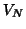 can be chosen to be for the form
can be chosen to be for the form
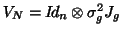 as in compound
symmetry, and similar techniques described for mixed models could be derived. This can be also
implemented as a three-stage model: seeing the random model as a GMANOVA model then resolved as a
two-stage model allow you to carry on levels in presence of a repeated design on the subjects
giving a third model. The estimation in multi-stage for multilevel models is valid as long as the
designs are well balanced which is the case in fMRI. Iterative GLS 30 may be needed
to improve estimation. Note a dense literature on multilevel modelling allows considerations of
more complex situations [9].
as in compound
symmetry, and similar techniques described for mixed models could be derived. This can be also
implemented as a three-stage model: seeing the random model as a GMANOVA model then resolved as a
two-stage model allow you to carry on levels in presence of a repeated design on the subjects
giving a third model. The estimation in multi-stage for multilevel models is valid as long as the
designs are well balanced which is the case in fMRI. Iterative GLS 30 may be needed
to improve estimation. Note a dense literature on multilevel modelling allows considerations of
more complex situations [9].



Next: Discussion and Conclusions
Up: tr00dl1
Previous: 2 and g groups
Didier Leibovici
2001-03-01