

Next: Using PTA-kmodes for PDY
Up: Multiway multidimensional data reduction
Previous: SVD-kmodes for and
Handling PTA-kmodes method
SAS/IML programs running with macro facilities have been written by the author to compute the
SVD-kmodes of a tensor of any order [13] with or without non-identity metrics
(R-functions are also available [14]). As stopping rule for the decomposition to
finish, one can ask for a maximum number of k-modes solutions at each level of the
algorithm, controlled by minimum amount of variability. Playing with these two sets of parameters
allows either to get as close as wished to the full decomposition, or to pick up interesting
Principal Tensors. Figure 1 shows what a PTA-3modes output listing looks
like. The 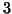 -modes solutions are noted vs111, vs222, ... the associated
-modes solutions are noted vs111, vs222, ... the associated 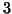 -modes
solutions to the first mode (X) are noted Xvs11, Xvs22... One must notice that
on the list of values the first associated solutions Xvs11 (or Yvs11, or Zvs11 )
are to be discarded in the decomposition as it is a repeat of vs111 because of the general
algorithm: let
-modes
solutions to the first mode (X) are noted Xvs11, Xvs22... One must notice that
on the list of values the first associated solutions Xvs11 (or Yvs11, or Zvs11 )
are to be discarded in the decomposition as it is a repeat of vs111 because of the general
algorithm: let
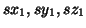 the first solution (i.e.
the first solution (i.e.
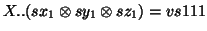 , the solutions associated to
, the solutions associated to 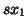 are obtained by the SVD-2modes of
are obtained by the SVD-2modes of
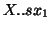 , therefore one finds again vs111 as the first singular values with solutions
, therefore one finds again vs111 as the first singular values with solutions 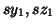 . Nonetheless it is interesting to keep these repetitions because of the information given by
the local decomposition (PCTloc: local percent of variability). PCT (respectively
PCTloc) are in the percent of sum of squares (equal to percent of variance if the tensor is
overall centred), then equals to the squared of the singular values divided by the total
(local) sum of squares. In a PTA-
. Nonetheless it is interesting to keep these repetitions because of the information given by
the local decomposition (PCTloc: local percent of variability). PCT (respectively
PCTloc) are in the percent of sum of squares (equal to percent of variance if the tensor is
overall centred), then equals to the squared of the singular values divided by the total
(local) sum of squares. In a PTA-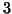 modes PCTloc refers to the usual percent of
variability for an SVD; in general total refers to the original tensor analysed and
local to the tensor currently decomposed i.e. associated solutions at a given
level.
modes PCTloc refers to the usual percent of
variability for an SVD; in general total refers to the original tensor analysed and
local to the tensor currently decomposed i.e. associated solutions at a given
level.
Figure 1:
Example of output
listing from PTA-3modes.
|
|
The notations are adapted for PTA-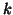 modes (notations are slightly different with the R functions
[14]),
for example for a tensor of order 5:
modes (notations are slightly different with the R functions
[14]),
for example for a tensor of order 5:
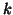 -modes solutions: vs11111, vs22222,...
-modes solutions: vs11111, vs22222,...
- associated
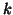 -modes first level: 1vs1111, 2vs1111..., 5vs1111, 1vs2222,...
-modes first level: 1vs1111, 2vs1111..., 5vs1111, 1vs2222,...
- associated
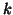 -modes second level: 1vs111,...,4vs666...,
-modes second level: 1vs111,...,4vs666...,
- associated
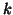 -modes third level: 1vs11,...,3vs66...
-modes third level: 1vs11,...,3vs66...
For each singular value, plots of components can then be produced using their normalised vector of
coordinates. For the same Principal Tensor, plots of different components are read simultaneously
as they correspond to the same singular value, but a basic rule must be kept to when interpreting
the result. The sign of pairs of vectors are arbitrary, like in PCA, but unlike in PCA a solution
is a triple of vectors (PTA-3modes) or a k-uple of vectors, then for example one has :
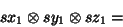 |
(12) |
So one must read the associations or oppositions of items from different components
(e.g. modalities, variables, spatial configuration) considering the product of the signs of
their coordinates, i.e. once the principal tensor has been mentally rebuilt. Plots of the
same component for different Principal Tensors can be produced but one must be aware of possible
non-orthogonality when they are not both 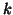 -modes Principal Tensors (remember the decomposition
is orthogonal on the whole space not ``completely" orthogonal in each space).
-modes Principal Tensors (remember the decomposition
is orthogonal on the whole space not ``completely" orthogonal in each space).


Next: Using PTA-kmodes for PDY
Up: Multiway multidimensional data reduction
Previous: SVD-kmodes for and
Didier Leibovici
2001-09-04
![\includegraphics[width=14cm]{pta3lis.ps}](img115.gif)