

Next: Handling PTA-kmodes method
Up: Multiway multidimensional data reduction
Previous: SVD within tensor algebra
Following a similar expression of a singular value one can write the maximisation problem to find
the first singular value of
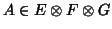 :
:
Solving the Lagrange problem allows to compute the first solution using the following iterative
algorithm (the iteration 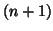 has three steps) where one can recognise a generalisation of the
transition formula (6) :
has three steps) where one can recognise a generalisation of the
transition formula (6) :
For the second and other solution an orthogonality constraint is added, but unlike for two modes
we do not have only the constraint of belonging to the orthogonal-tensorial of the first
principal tensor. For example one can put the constraint of belonging to the subspace
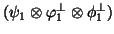 ; these solutions associated to
; these solutions associated to 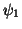 are easily
obtained from a SVD (SVD-(k-1)modes in general) after contracting the tensor
are easily
obtained from a SVD (SVD-(k-1)modes in general) after contracting the tensor 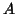 by
by
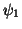 . The straightforward generalisation of (9), (10) and of the
second solution aspect, to the
. The straightforward generalisation of (9), (10) and of the
second solution aspect, to the 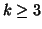 case can be found in [16].
Through this recursive algorithm, two types of principal tensors can be found: the
k-modes solutions when the constraint is expressed with an orthogonal-tensorial, and
their associated k-modes solutions obtained by SVD-(k-1)modes.
For example if
case can be found in [16].
Through this recursive algorithm, two types of principal tensors can be found: the
k-modes solutions when the constraint is expressed with an orthogonal-tensorial, and
their associated k-modes solutions obtained by SVD-(k-1)modes.
For example if 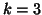 one has for each 3-modes solutions,
one has for each 3-modes solutions, 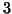 sets of associated
3-modes solutions: one set for each component of the 3-modes solution. If
sets of associated
3-modes solutions: one set for each component of the 3-modes solution. If 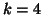 there are
two levels of associations: each 4-modes principal tensor will have
there are
two levels of associations: each 4-modes principal tensor will have 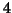 sets of associated
principal tensors, each set being obtained by the tensor product of a component
sets of associated
principal tensors, each set being obtained by the tensor product of a component 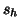 of this
4-modes principal tensor and the SVD-3modes solutions of
of this
4-modes principal tensor and the SVD-3modes solutions of 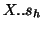 (where
(where 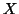 is the initial
tensor to analyse, and
is the initial
tensor to analyse, and 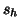 is the component in question), and then each SVD-3modes will
also have associated solutions as described before.
One can write the SVD-3modes of
is the component in question), and then each SVD-3modes will
also have associated solutions as described before.
One can write the SVD-3modes of 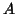 as an orthogonal decomposition :
as an orthogonal decomposition :
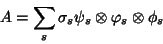 |
(11) |
Because of some good properties of this method, mainly a generalised Eckart-Young theorem
[16](i.e. nested model optimisation3, not usually found in other generalisation in the literature) we will confound
the PTA-kmodes and SVD-kmodes like we do with PCA and SVD. The singular values
obtained on k-modes solutions are treated in decreasing order, but for example, it happens
often that a singular value obtained with an associated solution of the first (or 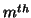 )
k -modes solution is bigger than the singular value obtained with the second (or next one)
k -modes solution. In the listings one must notice that for this reason, we kept the logical
order of computation instead of the ``true" decreasing order of the singular values.
)
k -modes solution is bigger than the singular value obtained with the second (or next one)
k -modes solution. In the listings one must notice that for this reason, we kept the logical
order of computation instead of the ``true" decreasing order of the singular values.


Next: Handling PTA-kmodes method
Up: Multiway multidimensional data reduction
Previous: SVD within tensor algebra
Didier Leibovici
2001-09-04