Using
![]() where
where
![]() gives
gives
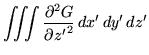 |
|||
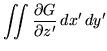 |
|||
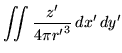 |
|||
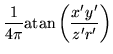 |
(22) |
By substituting this into equations 14 and 21, the
field ![]() can be calculated for this case. Note that provided
the
can be calculated for this case. Note that provided
the ![]() axis corresponds to the main static (constant)
axis corresponds to the main static (constant) ![]() field,
then this case is all that is required for the field calculation of a
non-conducting object.
field,
then this case is all that is required for the field calculation of a
non-conducting object.