

Next: Spatial
Up: Continuous Weights Mixture Model
Previous: Non-spatial without Class Proportions
We can approximate the distribution in
equation 5 by replacing the discrete labels,
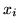 , with continuous weights vectors,
, with continuous weights vectors, 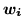 :
:
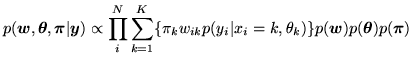 |
(13) |
where 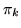 are the global class proportion parameters defined
in equation 4 and represent the proportion of each
class in the mixture model, and
are the global class proportion parameters defined
in equation 4 and represent the proportion of each
class in the mixture model, and
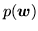 is given by
equations 10-12. Note
that when we infer on the posterior,
is given by
equations 10-12. Note
that when we infer on the posterior, 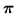 will depend upon
will depend upon
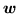 in same way that
in same way that 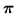 depends on
depends on 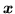 in the
discrete labels mixture model.
in the
discrete labels mixture model.
![]() , with continuous weights vectors,
, with continuous weights vectors, ![]() :
: