

Next: Class Distributions
Up: Continuous Weights Mixture Model
Previous: Non-spatial with Class Proportions
We can approximate the distribution in
equation 8 by replacing the discrete labels,
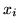 , with continuous weights vectors,
, with continuous weights vectors, 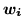 :
:
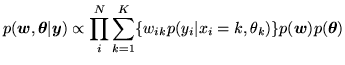 |
(14) |
where
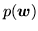 , is given by equation 10 with
, is given by equation 10 with
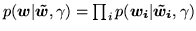 where as before
where as before
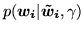 is specified by a
deterministic mapping between
is specified by a
deterministic mapping between
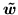 and
and 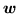 (the
logistic transform, equation 12).
(the
logistic transform, equation 12).
However, instead of equation 11,
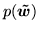 is now a continuous Gaussian conditionally
specified auto-regressive (CAR) or continuous MRF
prior (Cressie, 1993) on each of the
is now a continuous Gaussian conditionally
specified auto-regressive (CAR) or continuous MRF
prior (Cressie, 1993) on each of the 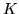 class maps, i.e.
class maps, i.e.
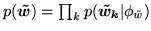 (where
(where
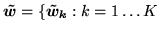 } and
} and
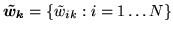 ) with:
) with:
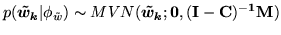 |
(15) |
where
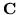 is an
is an
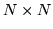 matrix whose (i,j)th
element is
matrix whose (i,j)th
element is 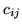 ,
,
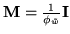 , and
, and
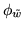 is
the MRF control parameter which controls the amount of spatial
regularisation. We set
is
the MRF control parameter which controls the amount of spatial
regularisation. We set 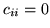 ,
,
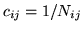 if
if 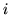 and
and
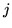 are spatial neighbours and
are spatial neighbours and 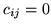 otherwise (where
otherwise (where
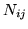 is the geometric mean of the number of neighbours for
voxels
is the geometric mean of the number of neighbours for
voxels 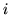 and
and 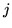 ) , giving approximately:
) , giving approximately:
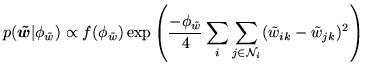 |
(16) |
How does this posterior approximation using
the continuous class weights vectors instead of
class labels allow us to adaptively determine the amount of
spatial regularisation? The answer is that
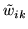 is a continuous random variable ranging
effectively between
is a continuous random variable ranging
effectively between 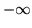 and
and 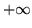 . Therefore,
unlike
. Therefore,
unlike 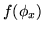 in
equation 6, the normalising
constant,
in
equation 6, the normalising
constant,
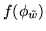 , in
equation 16 is known:
, in
equation 16 is known:
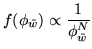 |
(17) |
and hence we can adaptively determine the MRF control parameter,
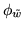 . To achieve this
. To achieve this
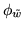 becomes a
parameter in the model, and equation 14
becomes:
becomes a
parameter in the model, and equation 14
becomes:
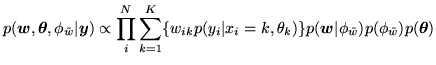 |
(18) |
where the prior
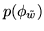 , is a non-informative
conjugate gamma prior:
, is a non-informative
conjugate gamma prior:
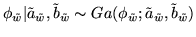 |
(19) |
In summary, we have approximated the discrete labels with vectors
of continuous weights which a priori approximate delta functions
at 0 and 1. Each vector of continuous weights deterministically
corresponds (via the logistic transform) to another vector of
continuous weights, which a priori are uniform across the real
line. As they are uniform across the real line these vectors of
continuous weights can be regularised using a spatial prior (a
continuous MRF) for which the amount of spatial regularisation can
be determined adaptively.
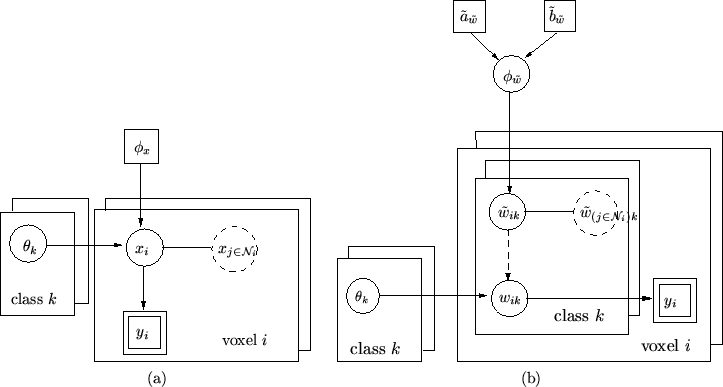
Figure 2 shows a graphical representation
of the discrete labels mixture model
(equation 8) and the continuous weights spatial
mixture model with adaptive spatial regularisation
(equation 14).
Figure 2:
Graphical representation of (a) the discrete labels
mixture model (equation 8), and (b) the
continuous weights spatial mixture model with adaptive spatial
regularisation (equation 14). Each
parameter is a node in the graph and direct links correspond to
direct dependencies. Solid links are probabilistic dependencies
and dashed arrows show deterministic functional relationships. A
rectangle denotes fixed quantities, a double rectangle indicates
observed data, and circles represent all unknown quantities.
Repetitive components are shown as stacked sheets. Dashed circles
represent nodes that really correspond to a different stacked
sheet, but which are shown on the top stacked sheet for ease of
display.
 |


Next: Class Distributions
Up: Continuous Weights Mixture Model
Previous: Non-spatial with Class Proportions
![]() , with continuous weights vectors,
, with continuous weights vectors, ![]() :
:
![]() is now a continuous Gaussian conditionally
specified auto-regressive (CAR) or continuous MRF
prior (Cressie, 1993) on each of the
is now a continuous Gaussian conditionally
specified auto-regressive (CAR) or continuous MRF
prior (Cressie, 1993) on each of the ![]() class maps, i.e.
class maps, i.e.
![]() (where
(where
![]() } and
} and
![]() ) with:
) with:
