

Next: Non-spatial with Class Proportions
Up: Continuous Weights Mixture Model
Previous: Continuous Weights Mixture Model
We are going to approximate the distribution in
equation 3 by replacing the discrete labels,
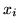 , with
, with
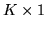 continuous weights vectors,
continuous weights vectors,
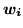 :
:
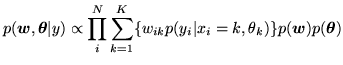 |
(9) |
where
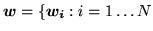 } and
} and
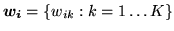 is the continuous weights
vector at voxel
is the continuous weights
vector at voxel 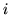 . Equation 9 only
approximates equation 3 if we apply certain
constraints to the continuous weights vectors. If we choose a
prior on the continuous weights vector,
. Equation 9 only
approximates equation 3 if we apply certain
constraints to the continuous weights vectors. If we choose a
prior on the continuous weights vector, 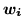 , with the
constraints that
, with the
constraints that
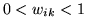 and
and
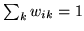 , then as
, then as
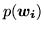 tends to delta functions at
tends to delta functions at 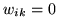 and
and
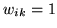 , then equation 9 will tend
to equation 3. Therefore, to apply these
constraints the prior we use is:
, then equation 9 will tend
to equation 3. Therefore, to apply these
constraints the prior we use is:
where:
and
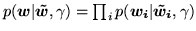 , where crucially
, where crucially
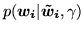 is a deterministic
relationship by which
is a deterministic
relationship by which 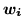 and
and
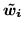 are
related by the logistic transform:
are
related by the logistic transform:
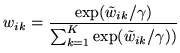 |
(12) |
The normalising constant in the logistic transform
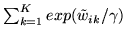 ensures that the condition
ensures that the condition
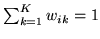 is met. This expression also ensures
that
is met. This expression also ensures
that
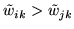 , if and only if
, if and only if
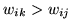 . Figure 1 shows how the
logistic transform produces an approximation to the delta
functions as
. Figure 1 shows how the
logistic transform produces an approximation to the delta
functions as 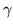 gets smaller. We fix the value of
gets smaller. We fix the value of 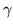 to 0.05 whilst bounding
to 0.05 whilst bounding
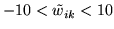 , this ensures
that we get the desired approximation to delta functions at 0 and
1, whilst ensuring that we can compute
, this ensures
that we get the desired approximation to delta functions at 0 and
1, whilst ensuring that we can compute
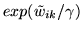 without causing overflow.
without causing overflow.
To summarise, we now have two vectors of continuous weights at each voxel,
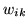 and
and
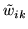 .
.
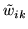 are weights which have a prior on them which
is uniform on the real line.
We then use the logistic transform to deterministically map
the weights
are weights which have a prior on them which
is uniform on the real line.
We then use the logistic transform to deterministically map
the weights
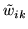 to
to 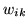 at each voxel.
Then,
at each voxel.
Then, 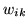 are the continuous weights which
represent approximations to
the discrete labels
with delta functions at 0 and 1.
are the continuous weights which
represent approximations to
the discrete labels
with delta functions at 0 and 1.
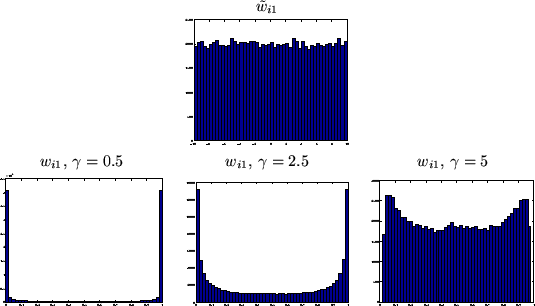
Figure 1:
Consider that we have the number of classes as 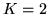 .
[top] shows samples from the
prior of
.
[top] shows samples from the
prior of
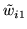 ,
,
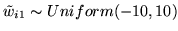 (samples from
(samples from
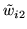 are
similar). [bottom] shows the samples from
are
similar). [bottom] shows the samples from
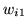 (
(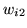 is similar), which the samples from the prior
of
is similar), which the samples from the prior
of
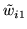 and
and
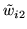 transform to under the logistic transform with
different values of
transform to under the logistic transform with
different values of 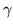 (equation 12). Hence, it can be seen
how this produces a prior for
(equation 12). Hence, it can be seen
how this produces a prior for
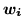 , which approximates the
desired delta functions at 0 and
, which approximates the
desired delta functions at 0 and 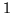 as
as 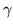 gets
smaller.
gets
smaller.
 |


Next: Non-spatial with Class Proportions
Up: Continuous Weights Mixture Model
Previous: Continuous Weights Mixture Model
![]() , with
, with
![]() continuous weights vectors,
continuous weights vectors,
![]() :
:
![]() and
and
![]() .
.
![]() are weights which have a prior on them which
is uniform on the real line.
We then use the logistic transform to deterministically map
the weights
are weights which have a prior on them which
is uniform on the real line.
We then use the logistic transform to deterministically map
the weights
![]() to
to ![]() at each voxel.
Then,
at each voxel.
Then, ![]() are the continuous weights which
represent approximations to
the discrete labels
with delta functions at 0 and 1.
are the continuous weights which
represent approximations to
the discrete labels
with delta functions at 0 and 1.
