


Next: Random subject effect
Up: Multi-subject analysis with GLM
Previous: Multi-subject analysis with GLM
Firstly, we will rewrite the single-group study. One has for each
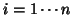 the GLM models:
the GLM models:
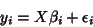 |
(30) |
with
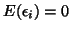 and
and
 . The case of auto-correlation
. The case of auto-correlation
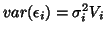 will be examined later on. It is rather straightforward to
recognise the fixed effect in the following model:
will be examined later on. It is rather straightforward to
recognise the fixed effect in the following model:
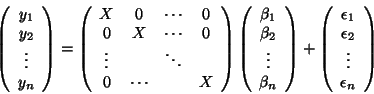 |
(31) |
or
 with obvious definitions for
with obvious definitions for 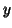 ,
, 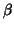 and
and 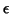 with
with
![$var(\epsilon)=diag({\sigma_{\epsilon_i}^2}_{[1..n]})\otimes I\!d_T$](img275.gif) .
One then derives easily the OLS for
.
One then derives easily the OLS for 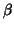 which gives the vector
of the OLS's from each model (30):
which gives the vector
of the OLS's from each model (30):
![\begin{displaymath}\hat{\beta}= \left ( \begin{array}{c }
\hat{\beta_1} \\
...
...[1..n]}}^2)\otimes(^tXX)^-=diag(var(\hat{\beta}_i)_{[1..n]})
\end{displaymath}](img276.gif) |
(32) |
Note that if one assumes that
 then:
then:
![\begin{displaymath}
\hat{\sigma}_\epsilon^2=\frac{^t\epsilon\epsilon}{trace(P_{...
...nT-n rank(X)}=\overline{\hat{\sigma}_{{\epsilon_i}_{[1..n]}}^2}\end{displaymath}](img278.gif) |
(33) |
which is the pooled estimate of variances, then:
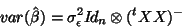 |
(34) |
In either cases testing 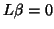 , with
, with
 , where
, where  is the contrast used on a
single model to assess the activation looked for, with the
statistic (19) will give the statistic used in
(4), and if
is the contrast used on a
single model to assess the activation looked for, with the
statistic (19) will give the statistic used in
(4), and if  is a matrix (
is a matrix (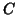 ) containing more than
one contrasts the
) containing more than
one contrasts the 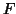 statistic (22) will be used.
statistic (22) will be used.



Next: Random subject effect
Up: Multi-subject analysis with GLM
Previous: Multi-subject analysis with GLM
Didier Leibovici
2001-03-01
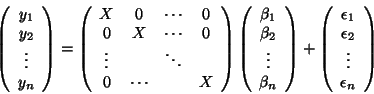
![\begin{displaymath}\hat{\beta}= \left ( \begin{array}{c }
\hat{\beta_1} \\
...
...[1..n]}}^2)\otimes(^tXX)^-=diag(var(\hat{\beta}_i)_{[1..n]})
\end{displaymath}](img276.gif)
![\begin{displaymath}
\hat{\sigma}_\epsilon^2=\frac{^t\epsilon\epsilon}{trace(P_{...
...nT-n rank(X)}=\overline{\hat{\sigma}_{{\epsilon_i}_{[1..n]}}^2}\end{displaymath}](img278.gif)