Temporal Autocorrelation in Univariate Linear Modelling of FMRI Data

FMRIB Technical Report TR01MW1
(A related paper has been accepted for publication in NeuroImage)

Mark W. Woolrich$^{1,2}$, Brian D. Ripley$^3$,Michael Brady$^2$ and Stephen M. Smith$^1$

1: Oxford Centre for Functional Magnetic Resonance Imaging of the Brain (FMRIB),
Department of Clinical Neurology, University of Oxford, John Radcliffe Hospital,
Headley Way, Headington, Oxford, UK
2: Medical Vision Laboratory, Department of Engineering Science,
University of Oxford, Oxford, UK
3: Department of Statistics, University of Oxford, Oxford, UK
Corresponding author -- Mark Woolrich: woolrich@fmrib.ox.ac.uk

Abstract:

In functional magnetic resonance imaging (FMRI) statistical analysis there are problems with accounting for temporal autocorrelations when assessing change within voxels. Techniques to date have utilised temporal filtering strategies to either shape these autocorrelations, or remove them. Shaping, or ``colouring'', attempts to negate the effects of not accurately knowing the intrinsic autocorrelations by imposing known autocorrelation via temporal filtering. Removing the autocorrelation, or ``prewhitening'' gives the best linear unbiased estimator, assuming that the autocorrelation is accurately known. For single-event designs, the efficiency of the estimator is considerably higher for prewhitening when compared with colouring. However, it has been suggested that sufficiently accurate estimates of the autocorrelation are currently not available to give prewhitening acceptable bias. To overcome this, we consider different ways to estimate the autocorrelation for use in prewhitening. Having performed high-pass filtering, a Tukey taper (set to smooth the spectral density more than would normally be used in spectral density estimation) performs best. Importantly, estimation is further improved by using nonlinear spatial filtering to smooth the estimated autocorrelation, but only within tissue type. 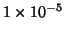Using this approach when prewhitening reduced bias to to close to zero at probability levels as low as $1\times10^{-5}$.