Multi-Level Linear Modelling for FMRI Group Analysis Using Bayesian Inference
FMRIB Technical Report TR03MW1
(A related paper has been accepted for publication in Neuroimage)
Mark W. Woolrich *, Timothy E.J. Behrens *, Christian F. Beckmann, Mark Jenkinson and Stephen M. Smith
Oxford Centre for Functional Magnetic Resonance Imaging of the Brain (FMRIB),
Department of Clinical Neurology, University of Oxford, John Radcliffe Hospital,
Headley Way, Headington, Oxford, UK
* First two authors contributed equally to this work
Corresponding author is Mark Woolrich:
woolrich@fmrib.ox.ac.uk
Functional magnetic resonance imaging studies often involve the
acquisition of data from multiple sessions and/or multiple subjects. A
hierarchical approach can be taken to modelling such data with a
General Linear Model at each level of the hierarchy introducing
different random effects variance components. Inferring on these
models is non-trivial with frequentist solutions being
unavailable. A solution is to use a Bayesian framework. One
important ingredient in this is the choice of prior on the
variance components and top-level regression parameters. Due to
the typically small numbers of sessions or subjects in
neuro-imaging the choice of prior is critical. To alleviate this
problem we introduce to neuro-image modelling the approach of
reference priors, which drives the choice of prior such that it is
non-informative in an information-theoretic sense. We propose two
inference techniques at the top-level for multi-level hierarchies
(a fast approach and a slower more accurate approach). We also
demonstrate that we can infer on the top-level of multi-level
hierarchies by inferring on the levels of the hierarchy separately
and passing summary statistics of a non-central multivariate
t-distribution between them.
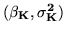 in the two-level model
in the two-level model